RAINBOWS

Rainbows Q&A

Explanation of a Rainbow...
What is a Rainbow?
When and where can I expect to see a rainbow?
What causes the rainbow’s circular shape?
What causes double rainbows?
Why are rainbows often incomplete?
Can I ever see an entire rainbow circle?
How big is the rainbow?
How many colours does a rainbow have?
Why is the sky inside the primary rainbow sometimes bright?
Why are bright rainbows most vivid near their base?
Why is the sky dark between the primary and secondary rainbows?
Why and when do red or orange rainbows occur?
What is a cloudbow, and when can I expect to see one?
Can I ever see rainbows on the ground?
What is a lunar rainbow and why is it white?
What are the pale green and purple arcs sometimes seen within the primary rainbow?
Why does a rainbow grow brighter and darker so quickly?
Can I touch the rainbow or reach its end?
Colour Terminology

Explanation of a Rainbow

A rainbow is a meteorological phenomenon that is caused by reflection, refraction and dispersion of light in water droplets resulting in a spectrum of light appearing in the sky.

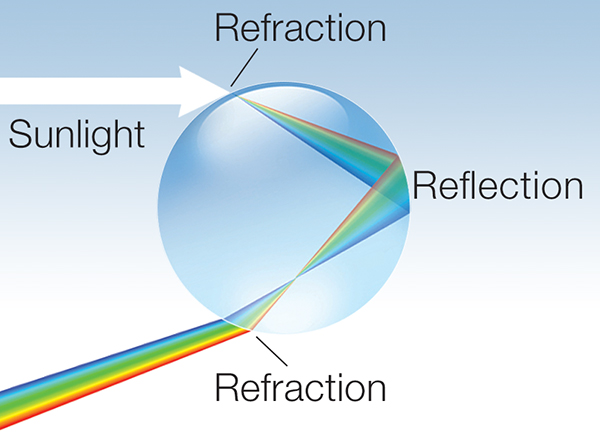
source: bom.gov.au

It takes the form of a multicoloured arc. Rainbows caused by sunlight always appear in the section of sky directly opposite the sun.

source: http://hyperphysics.phy-astr.gsu.edu/hbase/atmos/rbowpri.html

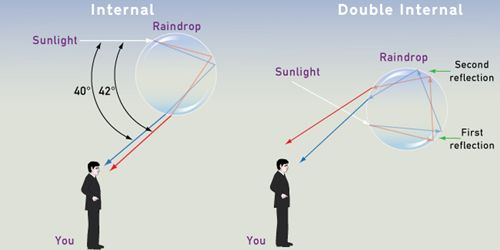
Rainbows can be full circles. However, the average observer sees only an arc formed by illuminated droplets above the ground, and centred on a line from the sun to the observer's eye. In a primary rainbow, the arc shows red on the outer part and violet on the inner side. This rainbow is caused by light being refracted when entering a droplet of water, then reflected inside on the back of the droplet and refracted again when leaving it. In a double rainbow, a second arc is seen outside the primary arc, and has the order of its colours reversed, with red on the inner side of the arc.

source: http://www.webexhibits.org/causesofcolor/13.htm

A rainbow is not located at a specific distance from the observer, but comes from an optical illusion caused by any water droplets viewed from a certain angle relative to a light source. Thus, a rainbow is not an object and cannot be physically approached. Indeed, it is impossible for an observer to see a rainbow from water droplets at any angle other than the customary one of 42 degrees from the direction opposite the light source. Even if an observer sees another observer who seems "under" or "at the end of" a rainbow, the second observer will see a different rainbow—farther off—at the same angle as seen by the first observer.

Rainbows span a continuous spectrum of colours. Any distinct bands perceived are an artefact of human colour vision, and no banding of any type is seen in a black-and-white photo of a rainbow, only a smooth gradation of intensity to a maximum, then fading towards the other side. For colours seen by the human eye, the most commonly cited and remembered sequence is Newton's sevenfold red, orange, yellow, green, blue, indigo and violet,remembered by the mnemonic, Richard Of York Gave Battle In Vain (ROYGBIV).

Rainbows can be caused by many forms of airborne water. These include not only rain, but also mist, spray, and airborne dew.A rainbow is not located at a specific distance from the observer, but comes from an optical illusion caused by any water droplets viewed from a certain angle relative to a light source. Thus, a rainbow is not an object and cannot be physically approached. Indeed, it is impossible for an observer to see a rainbow from water droplets at any angle other than the customary one of 42 degrees from the direction opposite the light source.

Even if an observer sees another observer who seems "under" or "at the end of" a rainbow, the second observer will see a different rainbow—farther off—at the same angle as seen by the first observer. Rainbows span a continuous spectrum of colours. Any distinct bands perceived are an artefact of human colour vision, and no banding of any type is seen in a black-and-white photo of a rainbow, only a smooth gradation of intensity to a maximum, then fading towards the other side. Rainbows can be caused by many forms of airborne water. These include not only rain, but also mist, spray, and airborne dew. source: Wikpedia

Q1: What is a rainbow?

A1: Observationally, the rainbow is a circular arc of several colours seen in rain or spray opposite the sun and centered around the shadow of your head. The rainbow’s colours are in concentric bands, and while they vary slightly from one bow to the next, the colours are always arranged in spectral order: red, orange, yellow, green, blue, and violet. While you are unlikely to see all of these colours in a given rainbow, their order does not change. For the inner (or primary) rainbow, red is on the outside; for the outer (or secondary) rainbow, red is on the inside.

rainbow

Optically, the rainbow is just a distorted image of the sun. Raindrops perform this rearranging of sunlight via reflection and refraction. Think of the drops as imperfect one-way mirrors: most light passes through them, but that forming the rainbow is reflected from their rear surfaces. In addition, as sunlight passes from air to water (or vice versa) it is deviated from its original path, with blue light being deviated more than red. As indicates, this combination of refraction and reflection occurs at each air-water boundary. However, the light forming the primary rainbow is that refracted on entering the drop, reflected at its rear and refracted a second time on exiting.

Q2: When and where can I expect to see a rainbow?

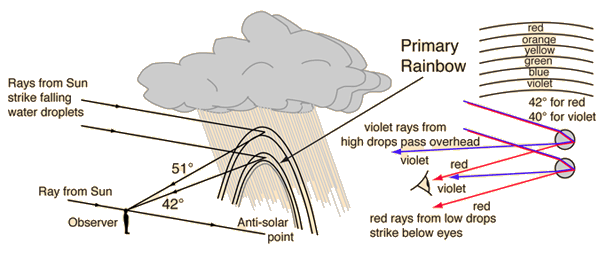
A2: You can see the rainbow whenever you look opposite the sun at sunlit raindrops (or spray drops). The rainbow occurs because raindrops do not scatter sunlight uniformly in all directions . Consider a ray passing through the middle of the drop. It is deviated by 180°, returning in the direction that it entered (ray Q in is closest to this ray). As rays strike the drop at ever more glancing angles, the combined refractions and reflection bend the rays through smaller and smaller angles. This does not continue indefinitely. One ray in particular is bent by 138°, the minimum deviation (ray M). Rays that enter the drop more obliquely are deviated by more than 138°. In contrast to other rays, this minimum deviation ray has a great many neighbors leaving the drop at nearly the same angle. It is this concentration of light 138° from the sun that forms the primary rainbow.

We translate the rainbow’s geometry to a more convenient reference point, the shadow of your head. Whenever you are illuminated by sunlight, the shadow of your head is 180° from the sun. The shadow of your head thus covers the antisolar point, the point directly opposite the sun. So the primary bow is a 42°-radius circle (180°-138° = 42°) centered on the antisolar point. All rays other than the minimum deviation ray simply add to the general brightness within this 42°-radius circle. Thus the sky within the primary rainbow may look bright compared to the brightness of the surrounding sky. By the same logic, the sky outside an intense secondary rainbow will be relatively bright. The reason is that rays exceeding the secondary rainbow’s minimum deviation are seen here (see A5 below). A natural corollary of this enhanced primary and secondary brightness is that the sky between bright rainbows looks dark (see A12 below).

Q3: What causes the rainbow’s circular shape?

A3: Many drops acting in concert cause the rainbow, and all of these must be at the same angle from the sun (i.e., the same angle from the antisolar point). Thus at any instant, only those drops before you that are on a 42° circle centered about the antisolar point can send you the concentrated rainbow light. These drops may be at any distance, but must be on the 42° circle. Put another way, the rainbow is a mosaic of light sent to you by many raindrops as they fall through the surface of the imaginary cone whose tip is at your eye and whose radius is 42° .

Q4: What causes the rainbow’s colours?

A4: The rainbow’s colours arise because the minimum deviation ray occurs at a slightly different angle for each colour. A prism’s refraction of white light into a spectrum is similar to the rainbow’s colour separation. Because blue light at minimum deviation is bent through a greater angle than red light, the red light is closer to the sun. As a consequence, red will be on the outside of the primary bow, closest to the sun, and blue will be toward the inside. Although an indefinite number of colours is possible, their sequence across the bow is not arbitrary. From the outside to the inside of the primary this spectral sequence is: red, orange, yellow, green, blue, violet.

A single fact explains the opposite colour orders of the secondary and primary rainbows: red light at minimum deviation is bent less than blue light, and thus red appears closer to the sun. However, because minimum deviation rays for the secondary are bent through more than 180° (see A5 ) “closer to the sun” now means that red appears on the secondary rainbow’s inner edge. In essence, deviating sunlight through more than 180° turns the rainbow colours inside out.

Q5: What causes double rainbows?

A5: The path of a light ray (ray M) that contributes to the outer (or secondary) rainbow. This ray is reflected twice within the drop. Because each internal reflection is paired with a refraction of light out of the drop, less light is available to form the secondary bow, and thus it is less intense than the primary. At minimum deviation, this secondary-rainbow light is bent through an angle of about 231°, which places the secondary rainbow 51° from the antisolar point (51°= 231°-180. Because the secondary rainbow is inherently dimmer than the primary, it may not always be visible. However, if the primary rainbow is very bright, look for its fainter secondary companion 9° outside it .

Q6: Why are rainbows often incomplete?

A6: Since the raindrops are falling, their supply must be uninterrupted if the bow is to last. Because the edge of a rain shaft can pass quickly across the position where the rainbow might occur, the bow can appear or disappear rapidly. As long as you see sunlit drops at the minimum deviation (or rainbow) angle, the bow will be with you. However, if any part of the circle where the rainbow can occur is devoid of either drops or direct sunlight, then that part of the bow will not form, which accounts for the partial bows we often see . Because the rainbow’s angular size and angular distance from the sun are fixed, we cannot see a rainbow in a distant shower if the sun is higher than 42° above the horizon (assuming that we are on level ground).

Q7: Can I ever see an entire rainbow circle?

A7: Yes, anytime that you can see many sunlit drops in all directions from the antisolar point, the rainbow circle will be complete. For example, you could see the rainbow circle from atop a mountain, high hill or building, or an airplane in flight. Less ambitiously, you can see the complete circle if you fill the air before you with sunlit spray that extends 42° from the antisolar point. Note that while this spray bow looks smaller than one seen in a distant shower, its angular size is the same.

Q8: How big is the rainbow?

A8: The primary rainbow’s angular radius is about 42° and its width is about 2°. The secondary’s angular radius is about 51° and its width is about 3°. Neither bow is an object, so neither has a linear size. However, we typically use our perception of an object’s angular size and our estimate of its distance from us to infer its linear size. Experience and expectation combine to make these inferences fairly accurate for familiar objects. The rainbow has a fixed angular size and we plausibly (but erroneously) equate its distance with that of the rain or spray in which we see the bow. Everyday experience tells us that, for a fixed angular size, objects that appear more distant are larger than those nearby. Despite the fact that the rainbow is not an object, we mistakenly assume that our usual rules relating angular and linear size apply. Thus rainbows seen in a distant shower are compellingly large, while those in a nearby spray seem small. Yet neither bow has a linear size, just a fixed angular size.

Q9: How many colours does a rainbow have?

A9: Quite literally, as many as you think you see, whether that number is three or 300! For good perceptual reasons, we recognize discrete bands of colour in the rainbow . However, the number of rainbow colours is actually indeterminate, with each colour blending smoothly into the next
.

Q10: Why is the sky inside the primary rainbow sometimes bright?

A10: See A2 above.

Q11: Why are bright rainbows most vivid near their base?

A11: Large raindrops flatten as they fall but smaller ones do not. As a result, all sizes of raindrops contribute to the rainbow near its base, and large drops make this part of the bow both bright and colourful. However, as we approach the top of the arch only small drops contribute to the rainbow, and these yield a less intense, more pastel bow.

Q12: Why is the sky dark between the primary and secondary rainbows?

A12: By definition, raindrops between the bows cannot send you any light that contributes to either the primary or secondary. In other words, light that has been internally reflected once (the primary) or twice (the secondary) by water drops does not reach you from this part of the sky, so the sky looks comparatively dark there. This dark band is known as Alexander’s dark band (Chapter 4) and is most evident if the primary and secondary bows are bright .

Q13: Why and when do red or orange rainbows occur?

A13: Near sunrise and sunset, scattering of sunlight over very long paths through the atmosphere can make direct sunlight noticeably reddish or orangish. Since direct sunlight shining on water drops causes the rainbow, the resulting rainbows will have a pronounced red or orange cast (see Greenler 1980, Plate 1-7; Minnaert 1993, Plates 11-12).

Q14: What is a cloudbow, and when can I expect to see one?

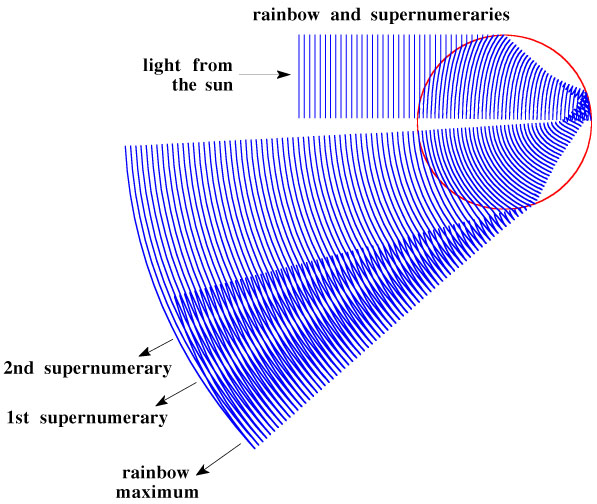
A14: A cloudbow is a water-drop bow caused by the same optics that generates the rainbow. However, cloud droplets are about 10 to 100 times smaller than raindrops or spray drops. An interference theory of the rainbow explains (1) the nearly colourless appearance of bows formed by these small drops, (2) the supernumerary bows that accompany both cloudbows and rainbows . A cloudbow may be visible when you fly above a deck of stratus clouds and can see your airplane’s shadow on them. Alternatively (and more arduously), you can see a cloudbow if you climb above a sunlit fog bank (i.e., stratus near the ground) that envelops the base of a hill or mountain. There you look for the cloudbow about 40° from the shadow of your head.

Q15: Can I ever see rainbows on the ground?

A15: Yes, if the ground is covered with sunlit dew, you may see the colourful dewbow. Like the rainbow, the dewbow’s light comes from a circular set of directions that are 42° from the antisolar point. However, because we know that dew lies on the ground before us, we have the compelling sense that the dewbow is a hyperbola (or an ellipse if the sun is high in the sky). (See Greenler 1980, p. 17, Plate 1-12 and Minnaert 1993, pp. 202-203.)

Q16: What is a lunar rainbow and why is it white?

A16: Like the sun, the moon can also generate rainbows. However, because moonlight is much less intense than sunlight, the lunar rainbow usually is too dim for us to see any colours in it. Recall that even under a full moon, objects that look vividly coloured during the day appear only in shades of gray. Thus the lunar rainbow is white Minnaert 1993, pp. 207-208).

Q17: What are the pale green and purple arcs sometimes seen within the primary rainbow?

A17: These are the supernumerary rainbows. Despite their superfluous-sounding name, they are an integral part of the rainbow . In fact, explaining how supernumeraries occur also explains the primary and secondary rainbows (see A14 above).

Q18: Why does a rainbow grow brighter and darker so quickly?

A18: See A6 above.

Q19: Can I touch the rainbow or reach its end?

A19: No. Because the rainbow is an image, not an object, you can never reach or touch it . However, in the same way that you can touch a mirror but not your image in it, you can touch the water drops that generate the bow. For example, if you make a rainbow in a sprinkler’s sunlit spray, you can certainly touch the spray. That is quite different from the impossible feat of touching the rainbow image.

About Colour Terminology

Given colour theory’s long and fractious history, it is not surprising that many different systems have arisen for describing colour. The table below lists several common colour schemes and their roughly equivalent terms. Entries in any given column may not be identical because the various systems themselves are not completely compatible. To further complicate matters, many other independent (although highly structured) colour-naming systems are used in commerce and industry. For thorough reviews of colour terminology, see Billmeyer and Saltzman (1981) and Zwimpfer’s beautifully illustrated chapter “Colour designation and organization”.

colour system	colour attributes
(informal)	colour	vividness or purity	brightness
CIE	dominant wavelength	colourimetric purity	luminance
artistic tradition	hue	saturation or tint	tone or lightness
Munsell System	hue	chroma	value

Bibliography -- Appendix

Billmeyer, Fred W., Jr., and Max Saltzman, 1981: Principles of Colour Technology (John Wiley and Sons, New York, 240 pp.; 2nd edition). Chevreul, Michel-Eugene, 1987: The Principles of Harmony and Contrast of Colours and Their Applications to the Arts, Faber Birren, ed. (Schiffer Publishing Ltd., West Chester, PA, 191 pp.; based on the English translation published by Henry G. Bohn (London, 1854)).
Greenler, Robert, 1980: Rainbows, Halos, and Glories (Cambridge University Press, Cambridge, UK, 195 pp.).
Herbert, Robert L., 1991: Georges Seurat, 1859-1891 (Metropolitan Museum of Art, New York, 450 pp.).
Minnaert, Marcel G. J., 1993: Light and Colour in the Outdoors (Springer-Verlag, New York, 417 pp.; English translation by Len Seymour).
Zwimpfer, Moritz, 1988: Colour, Light, Sight, Sense (Schiffer Publishing Ltd., West Chester, PA, n. p.).

Notes and References -- Appendix

[1]. Your hands and arms provide a built-in angular measure. Extend your arm straight and splay out the fingers on that hand, keeping your palm outward. The angular distance between the tips of your outstretched thumb and little finger is about 22°, so two hand spans cover 44°, slightly more than the primary rainbow’s radius. Thus if you put your thumb over your head’s shadow and measure a distance of two outstretched hand spans from it, you will be looking at the primary rainbow’s position.
[2]. A pigment mixture’s tone increases as black is added to it (i.e., lightness and tone change in opposite senses). Confusingly, “tint” is now sometimes a synonym for “hue.” (Chevreul 1987, p. 70 (paragraph 148); Herbert 1991, p. 381)
[3]. The Munsell System is a large collection of colour samples each of which differs from its immediate neighbor by a fixed perceptual interval of hue, chroma, or value. With its carefully measured colour samples, this practical and fairly rigorous system has long had many commercial applications. (Billmeyer and Saltzman 1981, pp. 28-30)