Mineral Optics
Mineral Optics
source adapted to html based on notes of Stephen A. Nelson, Tulane Universityincludes information written and developed by Charles Lewton-Brain, co-founder
of the Ganoksin Project for Jewellers and author. His web site is http://brainpress.com/index.
Light
Transparency
Reflection of Light
Refraction
Total Internal Reflection
Dispersion
Plane Polarized Light
Minerals
Crystal Symmetry
Crystal Systems
List of Major Gemstones
by Crystal System
Optical Effects in Gemstones
Lustres
Sheen
Interference of Light
Iridescence
Play of Colour
Diffraction
Opalescence
Chatoyancy
Asterism
Spectroscope

The optical characteristics and properties of gemstones often provide the fastest and best methods of identification. A certain amount of theory is necessary as optical principles determine cutting methods, gemstone attributes and the function of gem testing instruments.
Light
Light and our perception of it play a crucial role in our appreciation of and identification of gemstones. Visible light however comprises only a small part of what is referred to as the electromagnetic spectrum.While the wave or undulatory theory of light has been mostly superseded by the quantum (particle) theory the wave theory best serves the purpose of describing light for gemmology. We can consider the electromagnetic spectrum to consist of an infinite number of types of wavelengths, from short to very long. Different wavelengths have different powers of penetration dependent upon their length relative to the medium they pass through. X-rays for example with a wavelength near atomic sizes pass through or between most atoms. The amount passed depends upon the mass of the atom concerned. Dense atoms like lead for instance provide a screen against x-rays. An application of this is a test for diamonds, whether set or unset, where the suspect stones are x-rayed for ten seconds over photographic paper. Carbon atoms are small (low mass) and so diamond is transparent to x-rays and is invisible on the photograph while all diamond simulants show up as positive, opaque shapes.
A rough wavelength scale follows:
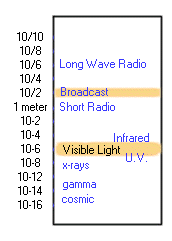
Note what a small portion of the spectrum comprises visible light. Light can be thought of as progressing outward in a single path (a ray). The ray forms a wave vibrating in all planes at right angles to the direction of travel, the line of the ray.
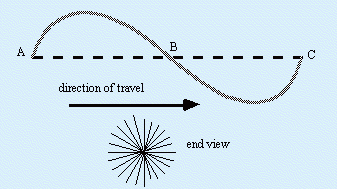
White light is composed of a mixture of a great many wavelengths each of which is perceived as a different colour. The wavelength of violet light for example is about half that of red light.
The wavelengths of white light may be divided into:
Red 700.0 nm to 640.0 nm
Orange 640.0 nm to 595.0 nm
Yellow 595.0 nm to 575.0 nm
Green 575.0 nm to 500.0 nm
Blue 500.0 nm to 440.0 nm
Violet 440.0 nm to 400.0 nm
Transparency
Refers to the ease with which light is transmitted through a substance. Classifications of transparency in cut gemstones include: 1. Transparent stones. An object viewed through the gem shows outlines clearly and distinctly (diamond, topaz, corundum).2. Semi-transparent. Blurred outlines of object but a great deal of light still passes through the stone, i.e. chalcedony.
3. Translucent. Some light passes through, no object can be seen through stone, i.e. opal, some jades, much cryptocrystalline quartz.
4. Semi-translucent. Light is only transmitted through edges, where they are thin, i.e. turquoise.
5. Opaque. No light passes through, i.e. malachite, pyrites.
Colour and degree of colour will affect transparency as will inclusions, flaws, etc. Quality will also affect it. The characteristics are subjective in nature and overlap exists.
Reflection of Light
If a ray of light falls onto a plane mirror the light is reflected away from the surface. The angle of incidence NOI equals the angle of reflection NOR and IO, NO and RO are in the same plane. All angles in optics are measured from the ‘normal’, an imaginary line at right angles to the surface at the point of incidence (where the light ray strikes the surface).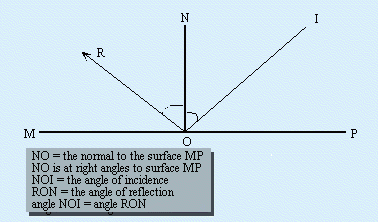
Refraction
A ray light entering an optically denser medium is bent (refracted) towards the normal. The greater the bending (refraction) for a given angle of incidence the greater is the refractive power of the stone.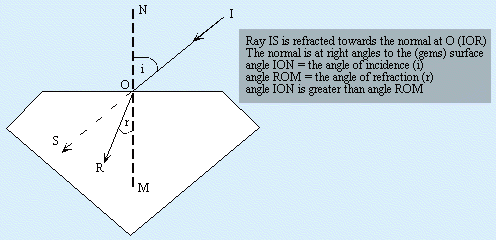
The cause of refraction is that the light waves (300,000 km/second) are slowed down as they enter the optically denser medium. In the 17th century Snell (Dutch scientist) described laws relating angles of incidence and refraction for two media. There is a constant ratio between the sines of these angles for any given two media. The constant ratio obtained is called the refractive index. Air is chosen as the rarer medium and yellow sodium light is the standard for refractive index measurements. Refractive index is a measure of a gem’s refractive power. It is the ratio of the sine of the angle of incidence divided by the sine of the angle of refraction when light passes from air into the denser medium.
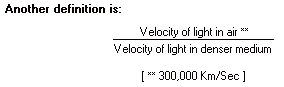
Gems refractive indices range from under 1.5 to over 2.8.
Total Internal Reflection
A ray passing in the opposite direction, from the denser to the rarer (gem to air) medium is bent (refracted) away from the normal.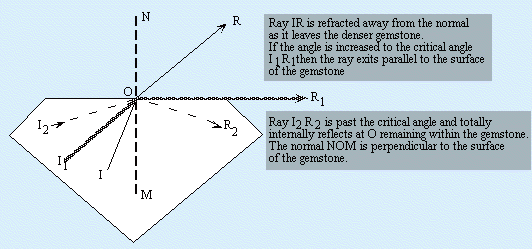
As the angle of incidence is increased the angle of refraction away from the normal increases until a point is reached when the ray I1OR1 exits parallel to the table of the stone. Any further increase in this angle causes the ray to be totally reflected back into the gem. Ray I2OR2 has been reflected back into the gemstone. This is called total internal reflection and the angle I1OM is called the critical angle for the medium in question. The brilliant cut of diamonds uses total internal reflection and the critical angle for diamond and air to ensure that all light entering the stone is totally reflected and passes out the table or crown facets of the stone. The critical angle is also what enables a refractometer to differentiate gemstones of different species.
Dispersion
A white light ray entering an optically denser medium and leaving by a plane inclined to that of entry will have its colours separated, analyzed, spread out. This is because each colour has a different wavelength and so is differently slowed down (refracted) by the medium. Red (longest wavelength) is slowed the least and violet (shortest wavelength) the most.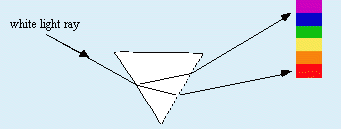
This spreading is termed dispersion. In gemstones the effect gives rise to the stone’s ‘fire’. It may be measured with complex equipment and numerical values given. The higher the number the greater the fire where the stone’s colour does not mask the effect, as in demantoid (green) garnet with a greater dispersion (.057) than diamond (.044). With practice and standard stones numerical estimates of dispersion may be made with the Hanneman/Hodgkinson slit technique.
Plane Polarized Light
When a light ray passes through a doubly refractive gemstone it is split into two rays with different amounts of refraction. Each ray is plane polarized, that is instead of the wave vibrating all directions about the line of the ray it vibrates in a single plane only. Each ray is plane polarized at right angles to the other. As each ray is differently refracted so it is differently absorbed by the stone and possesses in coloured gems a different hue or colour.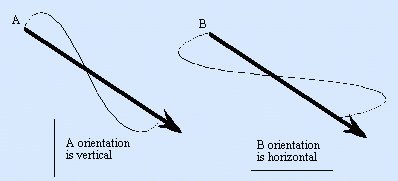
The Dichroscope picks up each ray at the same time and allows one to view them side by side. A simple dichroscope is a block of calcite with black paper glued to one end which has a small rectangular hole cut in it. The viewer sees two images because the light ray has been split by the high double refraction of calcite. Each image is of a different ray (each ray is also plane polarized at right angles to the other - this is what allows the calcite to present them separately). If a difference in colour exists it will be visible by comparison. One must always test in several directions. This can be of some use in identifying gemstones by their characteristic dichroic or trichroic colours but is usually used as a method of detecting double refraction. Presence of dichroism proves double refraction. Absence does not mean a material is not doubly refractive - it may be that the dichroism is very weak, or in transparent stones there is none evident. It can be used to find an optic axis. If three colours (trichroic) are seen it means the stone is biaxial. If two only are seen it is uniaxial. Transmitted, not reflected light must be used as reflected light may be partly polarized. Most natural corundum is cut with the table oriented to the optic axis and will show no dichroism through the table. Most synthetic corundum has the table parallel to the optic axis and dichroism is strongest through the table. This is then an indication of synthetic origin.
Minerals
A mineral may be defined as a homogenous substance produced by the processes of inorganic nature having a chemical composition and physical properties which are constant within narrow limits. Its structure is crystalline. It is composed of the same substance throughout. Except for impurities it has the same chemical formula for all specimens of the mineral. Its atoms usually have a definite and ordered crystal structure.What makes a mineral (or an organic product) a gemstone is cultural and partly subjective: beauty, durability and rarity.
Minerals often occur in geometrical forms bounded by plane surfaces. These are crystals and the internal structure determines properties which allow the identification of the gem material; its differentiation from other minerals, imitations and sometimes synthetics.
Crystals have:
- An orderly and symmetrical atomic structure.
- A definite external geometrical shape bounded by plane faces.
- Physical (and optical) properties which vary with direction.
Glass has:
- No regular atomic structure.
- No tendency to assume a definite external shape.
- Properties which are the same in all directions.
Crystalline Material:
Possesses the regular structure and directional properties of a crystal but not the regular geometrical shape. Also called massive. e.g. rose quartz.
Crypto-crystalline Material:
Material which consists of a multitude of tiny, often submicroscopic crystals. e.g. Chalcedony.
Crystal Symmetry
Crystal symmetry refers to the balanced pattern of the atomic structure which is reflected in the external (crystal) shape.Different species vary in the symmetrical arrangement of faces. These arrangements have certain 'planes' and 'axes' of symmetry.
These form part of the definition of the crystal system to which specific gemstones belong.
Plane of symmetry:
An imaginary plane dividing a body into two parts such that each is the reflected image of the other. Crystals may have more than one plane of symmetry. i.e. a cube has nine planes of symmetry.
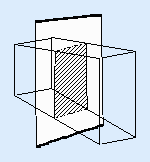
Axis of symmetry:
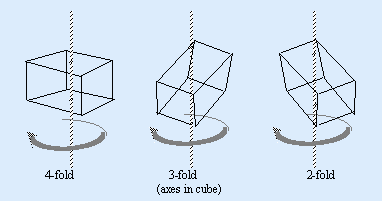
An imaginary axis is placed through a perfect crystal so that during a single rotation about this axis the outline of the crystal form appears identically more than once; 2, 3, 4 or 6 times.
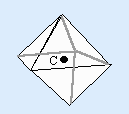
Centre of symmetry: (centro-symmetry)
Often present, it exists when every face of a perfect crystal is exactly opposite a similar face on the other side of the crystal.
An n-fold (Cn) proper rotation operation represents a counter-clockwise movement of (360/n)° around an axis through the object. If an n-fold rotation operation is repeated n times, then the object returns to its original position. Crystals with a periodic lattice can only have axes with 1-, 2-, 3-, 4-, and 6-fold symmetry axes. The following description of rotational symmetry operations is similar to that given by Prof. Stephen Nelson.3 In the following drawings, the symmetry axis extends perpendicular from the page.
1-Fold Rotation. A 1(E)-fold rotation operation implies either a 0° rotation or a 360° rotation, and is referred to as the identity operation.

2-Fold Rotation. A 2-fold(C2) rotation operation moves the object by (360/2) ° = 180 °. The symbol used to designate a 2-fold axis is a solid oval.

3-Fold Rotation. A 3-fold(C3) rotation operation moves the object by (360/3) ° = 120 °. The symbol used to designate a 3-fold axis is a solid equilateral triangle.

4-Fold Rotation. A 4-fold(C4) rotation operation moves the object by (360/4) ° = 90 °. The symbol used to designate a 4-fold axis is a solid square.

6-Fold Rotation. A 6-fold(C6) rotation operation moves the object by (360/6) ° = 60 °. The symbol used to designate a 6-fold axis is a solid hexagon.

Crystal axes: (Crystallographic axes)
To describe crystals imaginary lines are used intersecting at 0 (the origin). These are specific to the various crystal systems, intersecting at given angles and being of given lengths specific to each crystal system.
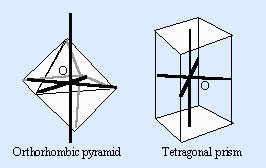
Origin:
The intersection of the crystal axes.
Habit:
Gemstone species tend to occur in characteristic shapes which relate to one or more of the forms common to the crystal system of the gemstone in question. The crystal form or forms which a gemstone most often appear are it's habit. e.g. diamond: octahedron, emerald: 6 sided prism.
Form:
Those faces of a crystal which are identically related to the crystal axes. When the space so defined is completely enclosed (cube, octahedron) it is a closed form. When identical faces do not completely enclose the space (four or six sided prism; top and bottom open) it is an open form.
Twinned crystals: (compound crystals)
A twin is a single crystal composed of two or more parts with any part in reversed structural orientation to the next, or interpenetrated.
Contact twin:
Sharing a common plane.

Interpenetrant twin:
Two individuals have grown from a common origin and appear to penetrate each other. e.g. cross stones.
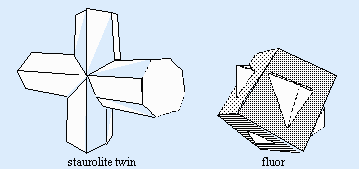
Lamellar twinning:
A series of contact twins often as extremely thin plates. Atoms in adjacent sheets are reversed, i.e. alternate plates are in the same order. This can give rise to special optical effects as in the feldspar labradorite.
Secondary twinning or parting:
The crystal is composed of very thin plates parallel to definite crystallographic directions. e.g. ruby, this gives rise to 'false cleavage'.
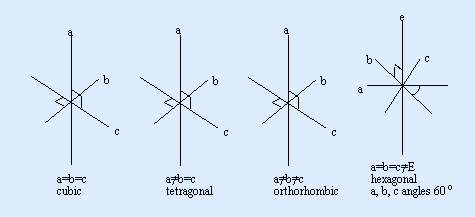
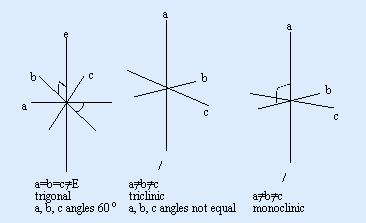
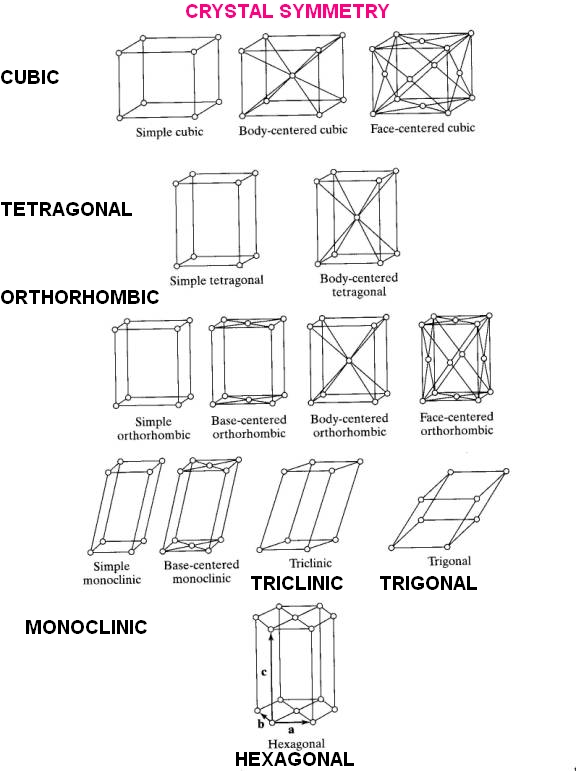
Crystal Systems
CubicThree crystal axes of equal length intersect at right angles to each other. e.g. diamond, spinel, garnets. Tetragonal Three axes intersect at right angles to each other. The vertical axis is of unequal length while the two horizontal axes are of equal length. e.g. zircon, rutile.
Hexagonal
Four crystal axes. Three are of equal length and intersect at 60o to form a horizontal plane which the fourth intersects at right angles. The vertical fourth is of unequal length and forms an axis of 6-fold symmetry. e.g. Beryl, apatite.
Trigonal
Four crystal axes. Three of equal length intersecting to form a horizontal plane which is intersected at right angles by the fourth axis. The vertical fourth is of unequal length and forms an axis of 3-fold symmetry. e.g. quartz, corundum, tourmaline, dioptase, haematite.
Orthorhombic (Rhombic)
Three crystal axes of unequal length interest each other at right angles. e.g. topaz, peridot, Chysoberyl, iolite, sinhalite, andalusite.
Monoclinic
Three axes. Two of unequal length intersect each other obliquely to form a plane which is intersected by the vertical third (of unequal length) at right angles. e.g. jadeite, nephrite, diopside, orthoclase feldspar, serpentine, sphene, malachite, spodumene.
Triclinic
Three axes of unequal length intersect each other at oblique angles. e.g. turquoise, labradorite.
NOTE: The Gemological Institute of America (GIA) system for crystal types differs from the above. Contact their web site for information on their courses, books and so on.
Crystal System Symmetry
Singly Refractive: Amorphous -- no crystal structureAmorphous
Uniaxial
The optic axis of the crystal is parallel to the main crystal axis. One direction of single refraction.
Biaxial
There are two directions of single refraction. (optic axes)
List of Major Gemstones by Crystal System
Cubic
Diamond (*Diamond simulants, man-made = uniaxial, = biaxial)
Sodalite
Fluorite
Spinel
Strontium Titanate*
Garnet
Yttrium Aluminate*
Lazurite (Lapis Lazuli)
Yttrium oxide*
Pyrites
Cubic Zirconia*
Tetragonal
Idocrase
Rutile
Zircon
Trigonal
Calcite (marble)
Quartz
Corundum
Rhodochrosite
Dioptase
Tourmaline
Hematite
Orthorhombic
Andalusite
Marcasite
Chrysoberyl
Peridot
Danburite
Sinhalite
Enstatite
Staurolite
Iolite
Topaz
Kornerupine
Zoisite
Monoclinic
Azurite
Nephrite
Diopside
Orthoclase Feldspar
Epidote
Serpentine
Euclase
Sphene
Jadeite
Spodumene
Malachite
Triclinic
Axinite
Kyanite
Microcline Feldspar
Plagioclase Feldspar
Rhodonite
Turquoise
Optical Effects in Gemstones
some of the terms used in discussing optical effects in gemstones.Lustres
Lustre (or the American spelling Luster) refers to the amount and quality of light reflecting from a gem’s surface to the eye. It is partially a subjective measurement but can be helped by comparison with a standard set of gems with known lustres. The hardness of a material, its refractive index and the degree to which it has been polished will have a bearing on the lustre. In general the harder a material is the higher the lustre, the softer it is the lower the lustre. The Americans and the British use slightly different nomenclature for lustres. The American Liddicoat terms the categories: “metallic, submetallic, adamantine, subadamantine, vitreous, subvitreous, waxy, greasy, silky, dull.” He goes on to say: ‘“The first three reflect the presence of refractive indices over the refractometer scale. Subadamantine suggests an index high on the scale; vitreous, midscale; and subvitreous, low. Waxy and greasy lusters are usually associated with poorly polished surfaces, while silky refers to stones with many needle like inclusions.” (Liddicoat, ‘Handbook of Gem Identification’, pp 216, 1993 ed.)Britain’s Webster says that many gems have a glassy or vitreous lustre. He gives examples and lists the lustre types as: “Metallic: silver, Adamantine: diamond, Subadamantine: demantoid garnet, Resinous adamantine: certain zircons, Vitreous: quartz, Resinous: amber, Silky: fibrous materials such as satin-spar, Pearly: usually seen only on cleavage faces, Waxy: turquoise”.
John Sinkakas makes a correlation between refractive index and luster (he’s American).
Refractive index is given first, then the corresponding comment on luster.
1.3-1.4 Poor reflections, inclined to be greasy or oily in appearance
1.5-1./8 Brightly reflective, like glass
1.6-1.9 Resinous in appearance
1.9-2.5 Very brightly reflective, adamantine, sometimes appearing as if the mineral is lightly coated with a metal film.
2.5 + Submetallic, bright luster, definitely metallic in appearance
(Sinkakas, John,. “Gemstone and Mineral Data Book”, pp 336)
Sheen
Sheen is due to the reflection of light from material below the surface of a gem. Moonstone, spectrolite and other feldspars are examples. Sheen in moonstone is also called schiller or adularescence. Pearls too have sheen as light reflects from below the surface of the pearl.Interference of Light
When a light ray strikes a surface composed of thin films part is reflected and part refracted into the films. The ray then reflects from film levels below the top surface and reenters the air. As it does so it interferes with; either intensifying or quenching certain wavelengths (colors) in other light rays reflecting from the top of the film. This produces color and light effects like that of oil on water, soap bubbles, Titanium and Niobium coloring, labradorite, tempering colors on steel and so on. In the diagram below a single ray is shown but in reality an infinite number of rays are doing the same thing simultaneously at all points on the surface of the partially reflective top layer or film.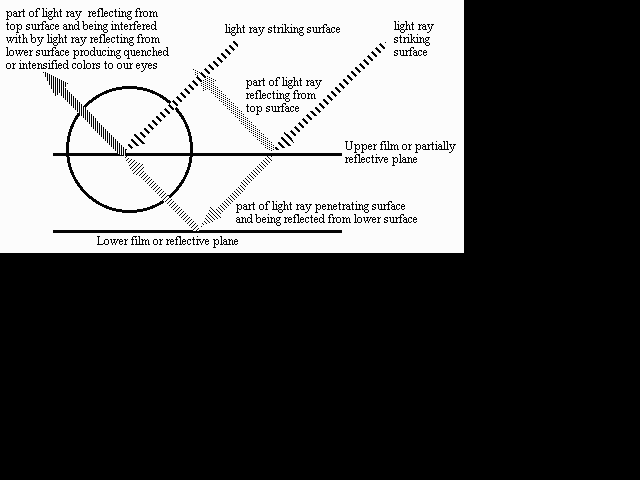
Iridescence
A general term for color effects produced by interference or by diffraction. Color play in opals, mother of pearl etc. are examples.Play of Colour
A term used to describe the colors seen in opal. This is caused by light diffraction from a regular structure of silica spheres in opals.Diffraction
When light passes over many tiny sharp edges or between many repeated points of differently refracting media an interference like phenomenon occurs; light is spread out into specific colors. You can see this on music CDs and sometimes on mesh between you and a light source. This principle is used in the diffraction grating spectroscope. This is what causes the play of color in opals, light being bent and diffracted as it passes innumerable regular stacked layers of minuscule silica gel spheres.Opalescence
The milkiness of opals. Sometimes it is used to describe play of color.Chatoyancy
When a gem material contains many minute fibrous inclusions oriented in one direction and it is cut en cabachon a streak of light or ‘eye’ can be seen at right angles to the direction of the inclusions. An example used to explain this is the light streak visible on a spool of silk thread or on an old 35 RPM record. Examples include chrysoberyl (cymophane), crocidolite (tigers eye) and quartz. Many gems can exhibit an ‘eye’ including tourmaline, beryl, nephrite, jadeite etc.Asterism
Star stones, these are most commonly sapphire and ruby but may include garnet, spinel, diopside and other gems. It is a special type of chatoyancy as the cause is due to many small fibrous inclusions oriented at set angles to each other. Examples are ruby (60o), garnet (70o). These inclusions in the case of corundum are all parallel to the lateral axes of the crystal and at right angles to the vertical crystal axis. When the stone is cut with the top of the cabachon dome oriented with the main crystal axis passing vertically through it and the silk inclusions parallel to the girdle of the stone asterism results. Each set of silk has a streak of light at right angles to it and a star is seen.Spectroscope
Along with the microscope and refractometer this is a major identification tool in gemology. As light passes through a gem the presence of certain chemicals will cause specific wavelengths of light to be absorbed. Instances also occur where wavelengths are intensified or the stone actually emits light (fluorescence wavelengths - rubies, spinel). When light is spread out by a prism or diffraction grating spectroscope into a wide band these absorbed wavelengths show up a lines or areas of darkness in the spectrum. While the actual wavelength numbers can be used in identification usually only a pattern of lines is used to identify the stone. It can be the fastest way of checking out large numbers of stones, even small ones, especially red gems, as spinel, ruby and tourmaline have distinctive spectra. It can be used to identify synthetic verneuil sapphire, blue synthetic spinel, almandine garnet to name a few. Note that British gemmologists have the red on the left and Americans have it on the right when looking at spectra. Here is an example of what the absorbtion spectrum pattern of a gem stone might look like through a spectroscope.Red is on the right in the diagram below.

Suggested Reading:
‘Gem Testing’ by Anderson and Webster,
‘Handbook of Gem Identification’ by Richard Liddicoat.
The latter has the best group of drawings available on what spectra look like, very fuzzy, hard to see at times.
Anderson, B.W. Gem Testing. London: Butterworths, 1980.
Liddicoat, Richard T., Jr. “Handbook of Gem Identification”. 12th ed. Santa Monica: Gemological Institute of America, 1993.
Sinkakas, John,. “Gemstone and Mineral Data Book: A Compilation of Data, Recipes, Formulas and Instructions for the Mineralogist, Gemologist, Lapidary, Jeweler, Craftsman and Collector”. Prescott, AZ: Geosciences Press, 1988.
Webster, Robert. “Gems: Their Sources, Descriptions and Identification”. Fourth ed. Rev. B.W. Anderson. London: Butterworths, 1983.

