Stars

ESA Logo

to Earth Processes / Structures / Extreme Weather...

Stars

source http://nineplanets.org
            https://alexgreenhead.wordpress.com/2014/04/20/fmp-main-infographic-development/
            http://peter-mulroy.squarespace.com/stars/
            https://www.osu.edu/
            http://www.ast.cam.ac.uk/~mjp/calc_parallax.html
            https://eaae-astronomy.org/WG3-SS/WorkShops/Triangulation.html

     see also the Sun...
     see also the Solar System...

Our sun
Stars in general
Stellar evolution
Life cycle of a star
Size of stars
Main Sequence stars
Red Giants and Super Giants
White Dwarfs
Pulsating Stars
Using pulsating stars to measure distance
Measuring distance to stars - parallax method


This is not an astronomy website. Our pages look at the stars from an earth science perspective.
Understanding the stars assists us in understanding the finite nature of energy and heavier elements in our own solar system and particularly on earth.
When we appreciate that the heavy elements we so much rely on here on earth are artifacts of collapsing of stars and supernova explosions, it makes us realise just how luck we are to be here and now.

Our Sun

The Sun is a star, with properties typical of those of billions of other stars in our Galaxy. This recognition resolved thousands of years of religious, philosophical, and scientific debate. To learn the fate of the Sun, on which we absolutely depend for survival, we must look to the stars.
         "Across the sea of space, the stars are other suns."--- Christiaan Huygens (1692)

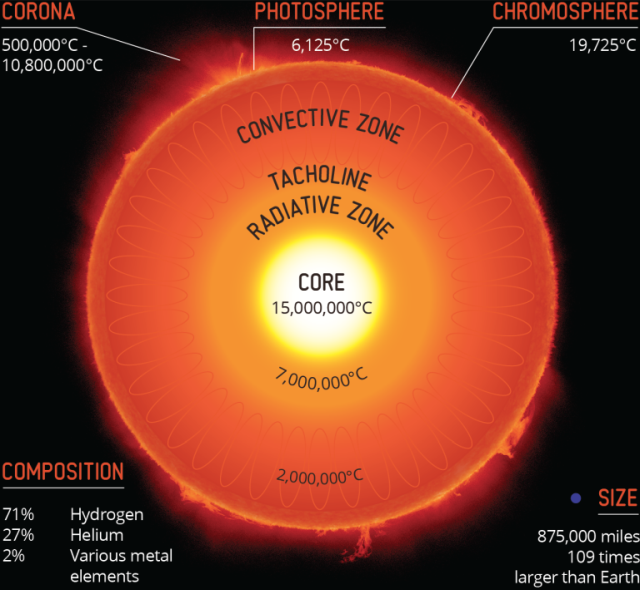
our sun

Stars in general

Stars generate their energy mainly by burning hydrogen in nuclear fusion reactions. Hydrogen is the most abundant element in the sun and in the universe, however, while the hydrogen supply is large; but it is nonetheless finite. This implies that all stars must evolve, that is to say when the hydrogen fuel supply is exhausted they will need to burn the next heaviest element which will change the temperature, size, colour and density of the star over time.
As a consequence, the favorable conditions in the Earth's biosphere cannot exist for ever and humans, or their descendants, will have to leave Earth at a predictable (if very distant) time in the future in order to survive.

An understanding of stellar evolution allows us to age-date the stars and thus establishes the basic time scale of the universe. The universe must be at least as old as the oldest stars.
The age of the Sun is 5 billion years. The oldest objects yet dated (globular star clusters---see below) are 13 billion years old. No identifications of significantly older stars have been made. The universe is therefore very ancient but had a finite beginning.
The age-dating of stars, and therefore the systems which contain them, is one of a handful of methods astronomers have for learning about the history of the universe.

All of the elements heavier than helium have been synthesized by nuclear reactions inside stars during their evolution particularly in supernovas. The Earth and all its inhabitants are made of atoms that passed through stars now long dead.
There could be no organic molecules without stellar nuclear-synthesis. For instance, all the atoms of carbon, nitrogen, oxygen, and phosphorus essential for DNA molecules are created inside stars (mostly stars at least 5 times more massive than the Sun).
Stars continuously form out of interstellar gas. Although the Sun is middle-aged, there are many "young" stars with ages of less than 10 million years within easy reach of your telescopes.
The Earth actually lies inside the Sun's (extended) atmosphere, so all forms of atmospheric activity on the Sun can potentially affect us.

progressive increase in star size
This image modified from the original . Original author is Dave Jarvis https://dave.autonoma.ca
The image is under his Creative Commons CC-BY-SA 3.0 Licence

Apparent brightness of stars (apparent magnitude) - how bright they are as viewed from earth

Absolute brightness of stars (absolute magnitude or luminosity) - how bright they would be if all viewed from the same distance (10 parsecs)
A parsec is a unit of distance which is defined in terms of the size of the Earth's orbit. It is 3.1 x 1013 km(!), 206,000 times the distance to the Sun, or about 3.25 light years (one light year is the distance light travels in a year

Star App.Mag. Distance (pc) Abs.Mag. Luminosity/Sun
Sun -26.7 4.84813×10-6 4.8 1
Sirius     (Alpha CanMaj) -1.4 2.64 1.5 22.5
Arcturus     (Alpha Boo) -0.05 11.25 -0.31 114
Vega     (Alpha Lyr) 0.03 7.76 0.58 50.1
Spica     (Alpha Vir) 0.98 80.5 -3.6 2250
Deneb     (Alpha Cyg) 1.3 3230 -8.7 250,000
Barnard's Star 9.5 1.82 13.2 1/2310

star size
This image modified from the original . Original author is Dave Jarvis https://dave.autonoma.ca
The image is under his Creative Commons CC-BY-SA 3.0 Licence

Temperature
We measure the surface temperatures of stars using their electromagnetic spectra, following experiments first done by the physicist Kirchhoff in the 19th century
Stars at the red end of the spectrum tend to be larger and cooler, white stars very small and hot and blue stars the hottest of all.
Our sun is an average size star in the yellow end of the spectrum.

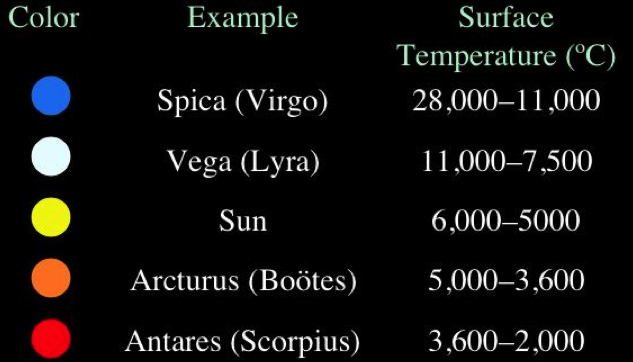
star colour and temperature


Stellar Evolution



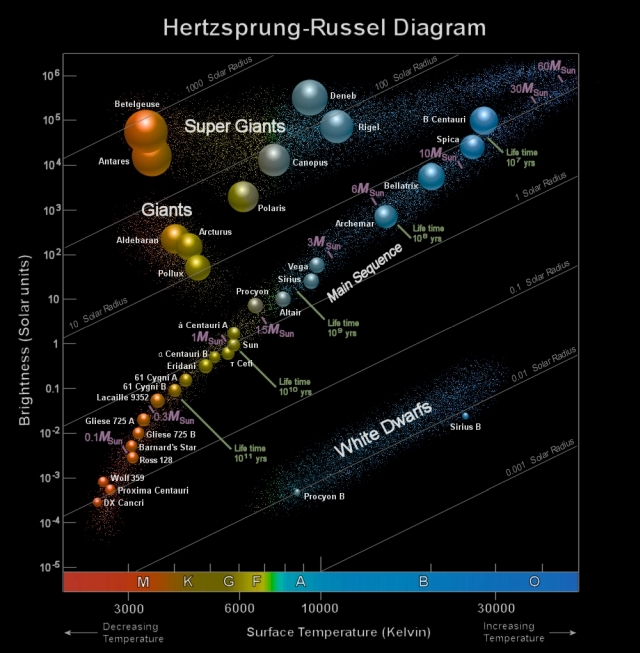
Stars are found in groups related to their mass, colour and tempertaure
In the Hertzsprung-Russell Diagram...

blue supergiant star


Life cycle of a star - two choices

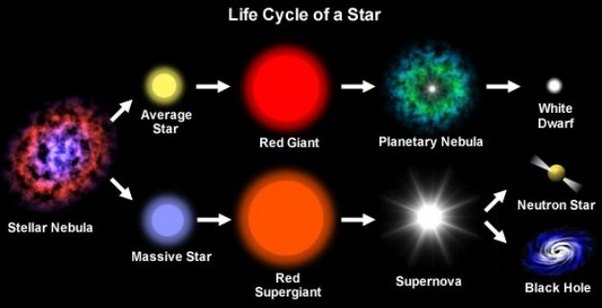
life cycle of a star

Starting as a cloud of dust a star can evolve in one of two basic way

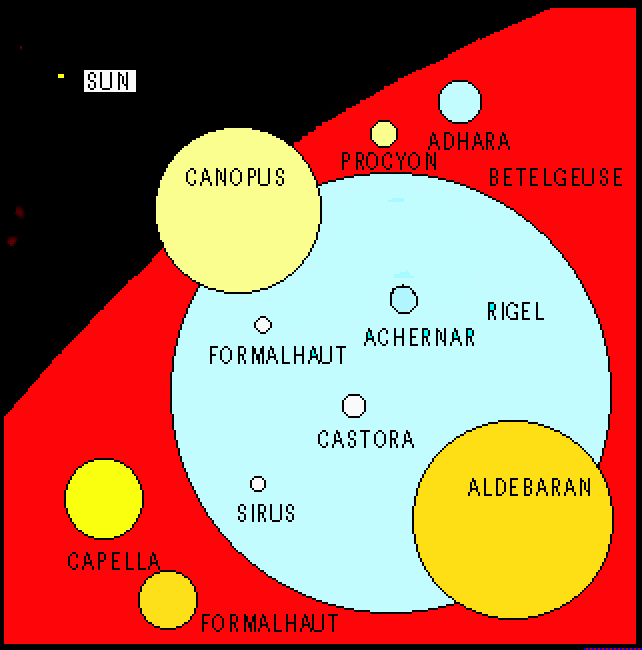
Size of stars

size of stars

Main Sequence

All main sequence stars (including the Sun) are powered by the fusion of hydrogen (H) into helium (He). Fusion of hydrogen requires temperatures of more than 10 million Kelvin. Above this temperature, the fusion rate is strongly dependent on temperature: a small increase in temperature results in a much higher fusion rate. Because fusion is so temperature-sensitive, in a main-sequence star, fusion of hydrogen into helium occurs only in the hot, dense central core.
All main sequence stars (including the Sun) are in hydrostatic equilibrium. That is, the inward force of gravity, which tends to compress the star, is balanced by the outward force due to the pressure

If you increase the mass of a star,  by pouring a little extra hydrogen gas onto it...
The higher mass will lead to higher compression --> which leads to higher central density and temperature --> which leads to much faster fusion --> which leads to much higher luminosity.

Because of the extremely sensitive dependence of the fusion rate on temperature, a small change in mass leads to a small change in the central temperature, but a very large change in the luminosity.
High mass main sequence stars have a shorter lifetime than low mass main sequence stars.

Stars don't blow themselves to bits in a runaway fusion reaction because of a physical relation among the pressure, temperature, and fusion rate which creates a natural buffer which keeps the center of the Sun (and the center of any other main sequence star) at a steady temperature.
 The "buffer" works like this...if you increased the fusion rate in a star's core:
  1. Core temperature increases
  2. Core pressure increases
  3. Core expands
  4. Core density & temperature decrease
  5. Fusion rate decreases
Thus, increasing the fusion rate sets a chain of events into action whose end result is to decrease the fusion rate again. 
If you decreased the fusion rate in a star's core:
  1. Core temperature decreases
  2. Core pressure decreases
  3. Core contracts
  4. Core density & temperature increase
  5. Fusion rate increases

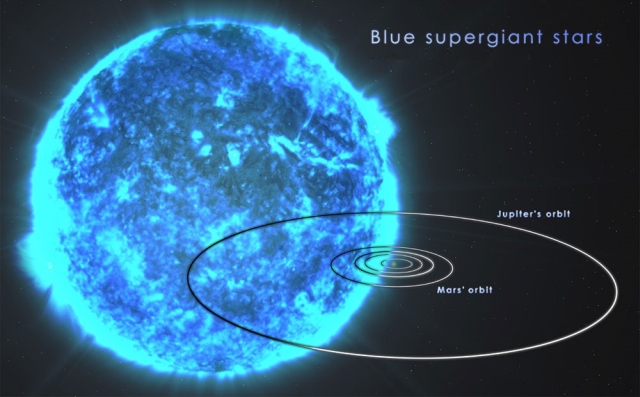
Red Giants and Super Giants

When a star exhausts the hydrogen in its core, it becomes a red giant or supergiant.
Mass of  > 0.4 M sun become hot enough to fuse helium into carbon.
Mass of  > 4 M sun become hot enough to fuse carbon into heavier elements.
Once a star has used up all the hydrogen in its core, fusion of hydrogen into helium stops. The core starts to contract again. As the core contracts, it releases energy. This energy heats up the layer immediately above the contracting helium core. The layer immediately above the core becomes hot enough to initiate the fusion of hydrogen into helium.

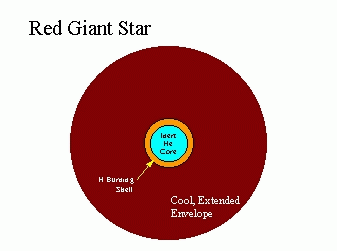
red giant star

The red giant star now has three main layers:
  1. Helium core (inner layer): Releases energy as it shrinks in radius.
  2. Fusion shell: Releases energy as it fuses hydrogen into helium.
  3. Hydrogen envelope (outer layer): Absorbs energy, and swells greatly in size.
These swollen stars, no longer on the main sequence, are now giants (if Magnitude < 8 Msun) or supergiants (if Magnitude > 8 Msun).
A giant's outer hydrogen envelope cools as it expands.
A giant becomes very large in radius and very cool -- hence the name "red giant".
Our sun will become a red giant in about 5 billion yearstime, its radius will increase to nearly 100 times its present size (engulfing Mercury as it expands) and its surface temperature will drop as low as 3000 Kelvin (from its present value of 5800 Kelvin).
In a red giant a huge, cool, low-density hydrogen envelope (with a density of about 0.1 kilograms/m3) encloses a small, hot, high-density helium core (with a density of about 1,000 tons/m3).

Once a giant or supergiant begins to fuse helium in its core, it has four main layers:
  1. Carbon (+oxygen) core: Releases energy as it shrinks in radius
  2. Helium fusion shell: Releases energy as it fuses helium into carbon (+oxygen)
  3. Hydrogen fusion shell: Releases energy as it fuses hydrogen into helium
  4. Hydrogen envelope: Still swollen in size

Once a supergiant becomes hot enough to fuse carbon into heavier elements, the carbon-oxygen core continues to shrink, becoming denser and hotter as it is compressed by gravity.
Once the central temperature reaches T > 600,000,000 Kelvin, carbon & oxygen can fuse into heavier elements, such as silicon, sulfur, and iron - a new energy source.
Our sun will never become hot enough to fuse into more massive elements.
Iron is the end of the line where fusion is concerned.
The iron nucleus (containing 26 protons) is the most tightly bound of all nuclei. The fusion of iron nuclei absorbs energy, instead of emitting energy.
The fusion process from hydrogen to iron emits energy, each step, as the nuclei become more massive, is less efficient.
As the star's core becomes hotter, and the fusion reactions powering it become less efficient, each new fusion fuel is used up in a shorter time.

White Dwarfs

Stars with initial masses  of M < 4 Msun will end their lives as white dwarfs.
The life stages of a low-mass star (one with M < Msun):
  1. Fusion of H into He in the star's core: main sequence -->
  2. Fusion of H into He in a shell outside the core: red giant --> 
  3. Fusion of He to C in the core, H to He in a shell: horizontal branch -->
  4. Fusion of He to C in a shell, H to He in a larger shell: asymptotic giant --> 
  5. branch No more fusion: formation of a white dwarf
A white dwarf is the end state of stars which start with a mass less than four times that of the Sun.

Pulsating Stars


Variable stars have luminosities which increase and decrease with a regular period
Main sequence stars have a nearly constant luminosity. (During the next five billion years, the Sun's luminosity will double; that's an increase of only 0.02% every million years.)
Some giants and supergiants have luminosities which regularly increase and decrease. The period of the luminosity fluctuations (that is, the time between peaks in the brightness) can range from a few hours to a few years.
Cepheid stars and RR Lyrae stars are variable because they pulsate in and out. The two most interesting types of variable star are Cepheid variables and RR Lyrae variables.
Cepheid variables are named after the star Delta Cephei (the fourth brightest star in the constellation Cepheus). The luminosity of Delta Cephei varies by a factor of two, with a period of 5 days. Polaris, the Northern Star, is also a Cepheid.
Cepheid variables have the following properties:
RR Lyrae variables are named after the star RR Lyrae, in the constellation Lyra.
RR Lyrae stars have the following properties:
Some simple thoughts on why stars pulsate...

Using pulsating stars to measure distance


The greater the luminosity of a Cepheid star, the longer its period of oscillation.
The Period-Luminosity relation is useful because it lets you measure the distance to Cepheid stars which are quite far away.
Because Cepheids are so luminous, they can be seen to large distances.
Parallaxes can be used to determine distances to 500 parsecs or so.
Period-luminosity relation can be used to determine the distance of a Cepheid about 40 million parsecs away.
This lets us find the distance to other galaxies in our neighborhood.

Measuring the distance to the stars - Parallax method

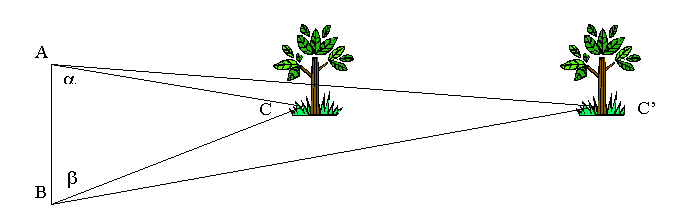
tree parallax example
Imagine measuring the distance of a tree without being able to walk to it (say because there is a river between you and the tree)
To find the distance you need to determine the shape and the dimensions of the triangle ABC.
When you measure AB (the baseline) and the two angles a (BAC) and b (ABC), the triangle ABC is completely known.
This area of mathematics involving working out triangles is called trigonometry and uses terms like sin / tan / cos (which have to do with the ratios of the lengths of the sides of a triangle and the angles)
Trigonometry is just a tool so all you need to do is plug your measurements into the formula.
From the diagram above...when the tree is farther away (C'), the angle at C becomes smaller and the shape of the triangle becomes different.
Stars are very far away so the angle is very very small.

To measure the distance to a star you use a huge triangle where one side of the triangle is twice the distance to our sun.
(This is like the line A-B in the tree example...)
Take a measure of the object now and then repeat the measure six months later when the earth is on the opposite side of the sun.
The object will appear to have moved relative to very distant stars in the background.
The angle is very small as the star is very distant  so it is measured in "seconds of arc" where 1 second of arc equals 1/3600 of a degree

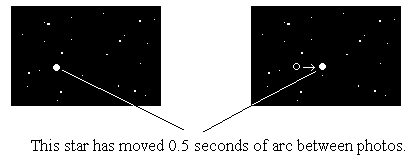
change in position of object over

          P = 0.5 / 2 = 0.25 seconds of arc.
        (1 second of arc (1") = 1 / 3600) degrees

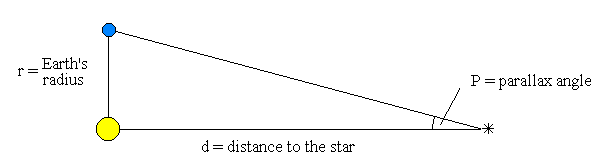
parallax calculation

The distance between the Sun and the star is :
             d = r / tan P
If P is 1 second of arc: d = 150 000 000 / tan 1" = 30 million million km

This distance is called one parsec and is a basic unit for measuring astronomical distances.

      Distance in parsecs = 1 / P in seconds of arc
                   d = 1 / P = 1 / 0.25 = 4
Therefore the star is four parsecs away.