Kepler's Laws of Planetary Motion
Kepler's Laws of Planetary Motion
condensed and adapted from the excellent mathematics and physics website of Dr. David P. SternTycho Brahe
Johannes Kepler
Ellipses
The First Law of Planetary Motion
Refining the First Law
Kepler's Second Law
Energy
The Mean Anomaly
The Third Law
Orbital Velocity
Third Law for Earth
Satellites
Applying Kepler's Third
Law
Tycho Brahe (1546-1601)
Tycho was a Danish nobleman interested in astronomy. In 1572 a "new star" (in today's language, a nova) appeared in the sky, not far from Polaris, outshining all others. Tycho carefully measured its position, then measured it again 12 hours later, when the the rotation of the Earth had moved the observing point to the other side of the Earth. Such a move was already known to shift the position of the Moon in the sky, helping astronomers estimate its distance. The position of the "new star" did not change, suggesting it was much more distant than the Moon

This event so impressed young Tycho that he resolved to devote himself to astronomy. The king of Denmark supported him and gave him the island of Hven to build an observatory, with the taxes of the island providing him with the funding. The telescope had not yet been invented, and all measurements were done by eye, aided by sights (similar to those used on guns) which could be slid around circles, marked in degrees. Tycho extended such methods to their ultimate limit, the resolution of the human eye, and his star charts were far more accurate than any earlier ones. He even measured and took into account the very slight shift of star positions near the horizon, due to the bending of light in the Earth's atmosphere, similar to its bending in glass or water. And his observations of the planets became the most stringent test of the theories of Copernicus and Ptolemy. Concerning those theories,
Tycho believed that all planets revolved around the Sun, but the Sun circled Earth. That view might have suited Denmark's Protestant church, for Martin Luther, founder of the Protestant doctrine, had rejected the views of Copernicus (who lived at the same time). Tycho's manners, however, were arrogant, and the residents of Hven complained about him, so that after the death of the king who was Tycho's patron, Tycho was forced to leave Denmark.
He settled in 1599 in Prague--now the Czech capital, then the site of the court of the German emperor Rudolf--and there he became court astronomer. It was in Prague, too, where a German astronomer named Johannes Kepler was hired by Tycho to carry out his calculations. When in 1601 Tycho suddenly died, it was Kepler who continued his work.

Johannes Kepler (1571-1630)
Kepler had studied astronomy long before he met Tycho: he favored the Copernican world-view and corresponded with Galileo.
Tycho's observations included some very accurate measurements of the position of the planet Mars, which did not agree with either Ptolemy or Copernicus. When Tycho died, Kepler got hold of those observations and tried to puzzle them out. In 1609, the same magic year when Galileo first turned his telescope towards the heavens, Kepler caught a glimpse of what he thought might be the answer. That was when he published his first two laws of planetary motion:
Planets move along ellipses, with the Sun at one focus.
The line from the Sun to the planet covers equal areas in equal times.
Each of these statement requires some explanation.Ellipses
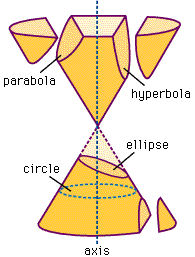
The ellipse, the shape of a flattened circle, was well known to the ancient Greeks. It belonged to the family of "conic sections," of curves produced by the intersections of a plane and a cone.
As the drawing on the left shows, when that plane is...
- perpendicular to the axis of the cone, the result is a circle.
- moderately inclined, an ellipse.
- inclined so much that it is parallel to one side of the cone, a parabola.
- inclined even more, a hyperbola.
Kepler's First Law
The Ellipse in Polar Coordinates
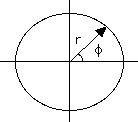
If all the values of (r,f) of a curve are related by some equation which can be symbolically written
r = r(f)
then the function r(f) is said to be the equation of the line, in polar coordinates. The simplest function is a constant number a, giving the line
r = a
The value of r equals a for any value of f. That gives a circle around the origin, its radius equal to a, shown in the drawing on the right above.
The Ellipse
Consider next the curve whose equation is
r = a(1- e2)/(1+ e cos f)
where the eccentricity e is a number between 0 and 1. If e = 0, this is clearly the circle encountered earlier.
How about other values? The function cos f represents a wave-like behavior (picture below), and as f goes through a full circle, it goes down, from +1 to 0, then -1, then up again to 0 and +1. The denominator also rises and falls as a wave, and it is smallest when cos f = -1 . Here is the table of the main values (360 is in parentheses, because it represents the same direction as 0 degrees):
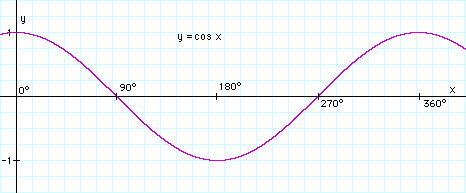
| f degrees | 90 | 180 | 270 | (360) | |
|---|---|---|---|---|---|
| cos f | 1 | 0 | -1 | 0 | 1 |
| 1 + cos f | 1 + e | 1 | 1 - e | 1 | 1 + e |
As long as e is less than 1, the denominator is always positive. It is never zero, so that for any f one can name, one can always find a suitable r. In other words, the curve goes completely around the origin, it is closed.
The expression (1 - e2) can be factored--that is, written as two expressions multiplied by each other ("the product of two expressions").
1 - e2 = (1 - e)(1 + e)
At some of the points on the above table, either (1 - e) or (1 + e) cancels the denominator, giving:
| f degrees | 0 | 90 | 180 | 270 | (360) |
|---|---|---|---|---|---|
| r | a(1 - e) | a(1 - e2) | a(1 + e) | a(1 - e2) | a(1 - e) |
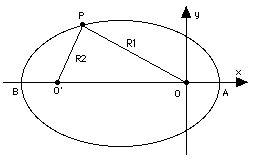
As mentioned in the preceding section a second focus O' can be drawn symmetrical to O, and the ellipse can be defined (its original definition, in fact) as the collection of points for which the sum R1+R2 of their distances from O and O' is always the same The longest dimension of the ellipse, its width AB along the line connecting the two foci, is its "major axis." Suppose (R1,R2) are the distances of A from the foci O and O'. Then R1 = OA =a(1 - e) is the smallest distance of the ellipse from O, R2 = O'A = OB (by symmetry) is the largest and therefore equals a(1 + e). But, OA + OB = AB, hence
AB = a(1 - e) + a(1 + e) = 2a
Hence the quantity a in the equation of the ellipse is known as semi-major axis. We can now state Kepler's law more precisely as "the square of the orbital period T is proportional to the cube of the semi-major axis a of its orbit around the Sun." The two quantities (a,e) completely define the ellipse. When that ellipse is the orbit of a planet or a satellite, they form two of the six orbital elements which define the state of the orbiting body. A third element, the mean anomaly M, specifies the position of the planet or satellite along the orbit, and the remaining three define the orientation of the orbit in 3-dimensional space.
Refining the First Law
Kepler's first law states:
"The orbit of a planet is an ellipse, with the Sun at one focus"
Actually, this is not 100% accurate. Imagine the planet magically getting heavier and heavier, while the Sun is getting lighter and lighter. At some point both of them would be equally heavy: could we then say which is orbiting around which?
To be fully accurate, the first law should have placed the focus of the orbital ellipse at the center of gravity of the planet-Sun system. (The center of gravity will be defined later, but intuitively, if the masses are very unequal, as with a planet and the Sun, it lies close to the center of the heavier object.) Because the Sun is so much heavier than the Mars, the effect on the orbit of Mars (which Kepler studied) was too small to be noted by him. Nevertheless, the Sun also moves in response to motions of its planets, and motions of this type have become an important tool in the search for planets outside the solar system.
An Earth-sized planet orbiting a distant star would be far too dim to be seen with any earthly telescope, especially against the glare of its sun, the star itself. However, as the planet goes around the orbit, its star also moves in a mirror image orbit around the common center of gravity. It is a much smaller orbit and a much slower motion, because the center of gravity is very close to the center of that star (in the Earth-Sun system, it is inside the Sun), but it can still be detected by subtle variations of the starlight.
Recently a few such planets have been found, but most are Jupiter-sized and none seems suitable for life.
Bodies in the solar system can also move in other conic sections, in parabolas or hyperbolas, whose equations resemble that of an ellipse, but have e equal to 1 or larger. Properly speaking, these orbits do not have a "semi-major axis," because they are not limited in size like ellipses but extend to infinity. Instead, we must write
r = p/(1 + e cos f)
which doe not raise any problems at e=1. Such bodies are not bound to the Sun, but are free to escape it. The denominator in the equation of the trajectory then becomes zero for some values of f, making its r infinite, and as the moving body approaches those values, it moves further and further away, with no limit. Comets in general have an eccentricity e close to 1, suggesting they have come from the very distant fringes of the solar system. The space probe Voyager 2 has e > 1 and is on its way out of the solar system, never to return.
Kepler's Second Law
The ellipse traced by a planet around the Sun has a symmetric shape, but the motion is not symmetric.
Think of a stone thrown upwards: as it rises it loses speed, then for an instant, at the top of the trajectory, it moves very slowly, and finally it comes down, gathering speed again. The motion of a planet around the Sun or of a scientific satellite around Earth follows different equations (though a connection exists), but in many respect it resembles that of the stone.
That is most evident if the orbit is elongated, that is, its eccentricity is not far from 1. As the planet or satellite rises in its orbit, it slows down, then as it returns, it speeds up again, moving at its fastest during its closest approach. That point of the orbit is called perihelion for a planet ("helios" is the Sun) and perigee for an Earth satellite ("gee" from "geo", denoting Earth-related).
After studying actual observations, mainly of Mars, Kepler proposed the following prescription for predicting the speeding-up and the slowing-down. Let a line ("radius vector") be drawn from the center of the Sun to the planet (or from the center of Earth to the satellite).
Kepler's Second law states:
"The radius vector sweeps equal areas in equal times"
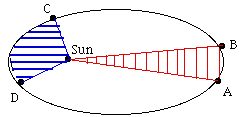 As an example, let the drawing on
the right represent the orbit of an Earth satellite, and let AB and CD be
the portions of the orbit covered in 3 hours near apogee and near perigee,
respectively. If then O is the Earth's center, the shaded areas OAB and
OCD are equal. What it means, obviously, is that CD is much longer than
AB, because near perigee the satellite moves much faster and it covers a
much greater distance in 3 hours.
As an example, let the drawing on
the right represent the orbit of an Earth satellite, and let AB and CD be
the portions of the orbit covered in 3 hours near apogee and near perigee,
respectively. If then O is the Earth's center, the shaded areas OAB and
OCD are equal. What it means, obviously, is that CD is much longer than
AB, because near perigee the satellite moves much faster and it covers a
much greater distance in 3 hours. Energy
Energy may be loosely defined as anything that can make a machine move. The forms of energy which power our machines are usually electricity or heat; light is another form, converted into electricity by the solar cells which power most satellites.
Gravity can also provide energy. The wheels of grandfather clocks are turned by weights which gradually descend to the bottom of the clock, at which point they have to be cranked up again, or else the clock stops. Thomas Jefferson, at his home near Charlottesville, Virginia, had a clock whose weights (hanging on the side of the room) were cannonballs strung on a rope, and to give the clock a 7-day range, a hole was cut in the floor allowing the balls to descend to the basement.
When a weight or cannonball is raised against the force of gravity, it has potential energy--energy by virtue of its position, proportional to the height to which it was raised. If the weight is dropped, it loses height and potential energy, but gains speed and kinetic energy, the energy due to speed of motion. Kinetic energy can be converted back to potential, as happens to a roller coaster after it passes the bottom of a dip and climbs up again.
A similar change occurs when a stone is thrown upwards with some velocity v. If its mass is m (mass will be defined later, for now view it as something related to weight), its kinetic energy can be shown to be
1/2 mv2
As it rises, v and the kinetic energy decrease, but this is matched by the growth of the potential energy
h m g
where h is the height in meters and g is a constant measuring the strength of the force of gravity: if m is in kilograms, h in meters and v in meters-per-second (written m/sec; walking speed is about 1-2m/sec), g is about 9.81.
The sum of the two is the total energy E and stays constant:
E = 1/2 mv2 + h m g = constant
As the stone rises, the kinetic part of its energy gets smaller and smaller, becoming zero when it reaches its highest point, where for a brief instant v = 0. On the downward trip, the opposite changes take place. In a later section we will come back to that formula and to the concept of energy.
For a satellite of mass m orbiting Earth (or for a planet around the Sun) a similar formula exists:
E = 1/2 mv2 - k m/r = constant
Here k is some other constant--actually, related to g, because both constants reflect the strength of the Earth's gravity (the exact value is k = gR2, where R is the radius of the Earth, in meters). Don't let the minus sign confuse you: as the satellite rises, r increases, k m/r becomes smaller, but -k m/r becomes bigger, it is less negative than near Earth. This equation shows why the satellite's speed decreases as it moves away and grows as it comes back.
Suppose the satellite has just enough velocity to escape Earth's gravity altogether (the "escape velocity" V). Then far from Earth, where k m/r is close to zero, its kinetic energy would also be exhausted, that is, v = 0. Since the sum E is the same everywhere, this suggests that for the space probe which just barely escapes the Earth's gravity, E=0. From that
V2 = 2k/R = 2 g R
With g = 9.81 and R =6 371 000 meter on finds V to be about 11200 m/sec.
The Mean Anomaly
Earlier it was stated that a third orbital element is needed to specify where in its orbit is the satellite located. Since the equation of the orbital ellipse is
r = a(1 - e2)/(1 + e cos f)
each value of the angle f --called the "true anomaly"--specifies a position along the orbit. One could therefore use the true anomaly as third orbital element.
The true anomaly f varies periodically around the orbit, quickly near perigee and slowly near apogee. Kepler's second law tells us everything about this variation and should allow us to obtain a formula that gives the way f varies with time t. Unfortunately, no neat way exists for expressing that formula.

The simplest way of expressing f is to use two auxiliary angles, which like f increase by 360 degrees each orbit, the "eccentric anomaly" E (the letter here has nothing to do with energy) and the "mean anomaly" M; an equation then exists connecting f and E, and another that connects E and M. The great virtue of M is that it grows in proportion to the time t:
M = M(0) + nt
where M(0) is the value of M when t = 0 and n is a constant (related to the constant appearing in Kepler's third law). The mean anomaly is what is counted as the third orbital element.
If one wishes to predict the position of a satellite in its orbit at some time t, assuming the elliptical motion of Kepler's laws is good enough for that prediction (neglecting the pull of the moon, friction of the upper atmosphere etc. ) the first step is to derive M from the above formula. Then E is derived from E, and finally f from E, tasks which electronic computers handle quite easily (though at one time, those calculations were done on paper, not nearly as quickly or easily). The formula for r then gives the position of the satellite in its orbit; all that the computation requires are the elements a, e and M(0), the mean anomaly at t=0.
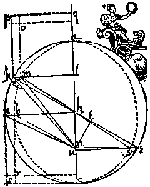
Below, a drawing of the orbit of Mars, from Kepler's writings
Kepler's Third Law
Kepler's Third Law States:
The square of the orbital period of a planet is directly proportional
to the cube of the semi-major axis of its orbit.
This captures the relationship between the distance of planets from the Sun, and their orbital periods.
All these intersections are easily produced by a flashlight in a moderately dark room . The flashlight creates a cone of light and when that cone hits a wall, the shape produced is a conic section--the intersection of the cone of light with the flat wall. The axis of the flashlight is also the axis of the cone of light. Aim the beam perpendicular to the wall to get a circle of light. Slant the beam: an ellipse. Slant further, to where the closing point of the ellipse is very, very far: a parabola. Slant even more, to where the two edges of the patch of light not only fail to meet again, but seem to head in completely different directions: a hyperbola.
After Tycho's death, Kepler became the court astronomer, although the superstitious emperor was more interested in astrology than in the structure of the solar system. In 1619 Kepler published his third law: the square of the orbital period T is proportional to the cube of the mean distance a from the Sun (half the sum of greatest and smallest distances). In formula form
T2= k a3
with k some constant number, the same for all planets. Suppose we measure all distances in "astronomical units" or AUs, with 1 AU the mean distance between the Earth and the Sun.
Then if a = 1 AU, T is one year, and k with these units just equals 1, i.e. T2= a3.
Applying now the formula to any other planet, if T is known from the observations of many years, the planet's a, its mean distance from the Sun, is readily derived. Finding the value of 1 AU in miles or kilometers, that is, finding the actual scale of the solar system, is not easy. Our best values nowadays are the ones provided by space-age tools, by radar-ranging of Venus and by planetary space probes; to a good approximation, 1 AU = 150 000 000 km.
| Kepler's 3rd Law T in years, a in astronomical units; then T2 = a3 Discrepancies are from limited accuracy |
||||
|---|---|---|---|---|
| Planet | Period T | Dist. a fr. Sun | T2 | a3 |
| Mercury | 0.241 | 0.387 | 0.05808 | 0.05796 |
| Venus | 0.616 | 0.723 | 0.37946 | 0.37793 |
| Earth | 1 | 1 | 1 | 1 |
| Mars | 1.88 | 1.524 | 3.5344 | 3.5396 |
| Jupiter | 11.9 | 5.203 | 141.61 | 140.85 |
| Saturn | 29.5 | 9.539 | 870.25 | 867.98 |
| Uranus | 84.0 | 19.191 | 7056 | 7068 |
| Neptune | 165.0 | 30.071 | 27225 | 27192 |
| Pluto | 248.0 | 39.457 | 61504 | 61429 |
Not only were Kepler's laws confirmed and explained by later scientists, but they apply to any orbital system of two bodies--even artificial satellites in orbit around the Earth. The constant k' for artificial satellites differs from k obtained for planets (but is the same for any satellite). By Kepler's formula
T = SQRT (k' a3)
where SQRT stands for "square root of" (the world-wide web does not offer more specific symbols). If T is measured in seconds and a in Earth radii (1 RE = 6371 km = 3960 miles)
T = 5063 SQRT (a3)
Besides the Moon, Earth now has many artificial satellites, put up by us earthlings for a variety of purposes. The calculation applied by Newton to the Moon can also be used for them.
Orbital velocity
Suppose the Earth were a perfect sphere of radius 1 RE = 6 317 000 meters and had no atmosphere. In principle, a satellite could then orbit just above its surface. The Earth would pull it downwards with a force F = mg, and because of the direction of this force, any accelerations would be in the up-down direction, too.If the satellite is in a stable circular orbit and its velocity is V, then F supplies just the right amount of pull to keep the motion going. Which means
mg = F = mV2/RE
Dividing both sides by m shows that the mass of the satellite does not matter, and leaves
V2/RE = g
Multiplication of both sides by RE: gives
V2 = (g) (RE) = (9.81) (6 371 000) = 62 499 510 (m/sec2)
V = 7905. 66 m/sec = 7.90566 km/s = Vo
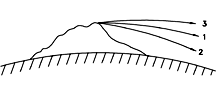
This is the velocity required by the satellite to stay in its orbit ("1" in the drawing). Any slower and it loses altitude and hits the Earth ("2"), any faster and it rises to greater distance ("3"). For comparison, a jetliner flies at about 250 m/sec, a rifle bullet at about 600 m/sec. We again need a notation for square root. Since the HTML language does not provide one, we use the notation SQRT found in some computer languages.
The square root of 2, for instance, can be written
SQRT(2) = 1. 41412. . .
If the speed V of our satellite is only moderately greater than Vo curve "3" will be part of a Keplerian ellipse and will ultimately turn back towards Earth. If however V is greater than 1. 4142. . .times Vo the satellite has attained escape velocity and will never come back: this comes to about 11.2 km/sec.
Kepler's Third Law for Earth Satellites
The velocity for a circular Earth orbit at any other distance r is similarly calculated, but one must take into account that the force of gravity is weaker at greater distances, by a factor (RE/r)2.
We then get
V2/r = g (RE r)2 = g RE2/r2
Let T be the orbital period, in seconds. Then (as noted earlier), the distance 2 pr covered in one orbit equals VT
| VT | = 2 p r | |
| V | = 2 p r/T | |
| V2 | = 4 p2r2/T2 | > |
| V2/r | = 4 p2r/T2 |
and by the earlier equality
4 p2r/T2 = g RE2/r2
Get rid of fractions by multiplying both sides by r2T2
4 p2r3 = g RE2 T2
To better see what we have, divide both sides by g RE2, isolating T2:
T2 = (4p2/g RE2) r3
What's inside the brackets is just a number. The rest tells a simple message--T2 is proportional to r3, the orbital period squared is proportional to the distance cubes. This is Kepler's 3rd law, for the special case of circular orbits around Earth.
Applying Kepler's Third Law
r circular orbits around Earth, we foundT2 = (4p2/g RE2) r3
with T in seconds and r in meters. The distance of a satellite from the center of Earth in meters is an inconveniently big number, even before we raise it to the 3rd power. We may however multiply the expression on the right by (RE3/RE3) = 1 and then rearrange the terms:
T2 = (4p2/g RE2) (RE3/RE3) r3 = (4p2RE/g) (r/RE)3
The ratio r' = (r/RE) is the orbital distance measured in units of the Earth's radius. That number is usually between 1 (at the Earth's surface, r = RE) and 60 (at the Moon's orbit, r ~ 60 RE).
Also, that ratio is always the same, whether r and RE are in meters, yards or nautical miles, as long as both r and RE are measured in the same units.
The other term is calculated below, with multiplication denoted by blank spaces between parentheses; you may check it with your calculator.
(4p2RE/g) = (4) (9.87) (6 371 000)/9.81 = 25 638 838
Using computer notation for the square root
SQRT (25 638 838) = 5063.5
From this
T2= (5063.5)2 (r')3
T= 5063.5 seconds SQRT(r')3 = 5063.5 sec r' SQRT(r')
This is the practical form of Kepler's 3rd law for Earth satellites. Our imagined satellite skimming the surface of the Earth (r' = 1) has a period
T = 5063.5 sec = (5063.5/60) minutes = 84.4 minutes
The space shuttle must clear the atmosphere and goes a bit higher.
Say it orbits at
r' = 1. 05, with SQRT(r') = 1. 0247
. Then
T = (5063.5) (1.05) (1.0247) = 5448 seconds = 90.8 minutes
International communication satellites are in the equatorial plane of the Earth and have orbits with a 24-hour period. As the Earth rotates, they keep pace with it and always stay above the same spot. What is their distance?
Here T is known and we need to find r':
T = 24 hours = 86 400 sec = 5063.5 SQRT(r')3
SQRT(r')3 = 86 400/5063.5 = 17.0632
If all numbers on the last line are equal, their squares are equal, too
(r')3 = (17.0632)2 = 291.156
Now you need a calculator able to derive cubic roots (or else, the 1/3 = 0.333. . . power).
This gives
r' = 6.628 earth radii
as the distance of "synchronous" satellites.
The satellites of the global positioning system (GPS), by which a small, handheld instument can tell one's location on the globe with amazing accuracy, are in 12-hour orbits.

