Rock and Fossil Age Dating Exercise
Rock and Fossil Age Dating Exercise
Exercise for determining the age of rocks and fossils (for students 12-14 years)
by Frank K. Mckinney Berkley University
Purpose and objectives
Materials required for each group
Part 1: Determining relative age of the rocks
Part 2: Radiometric age dating
Part 3: Putting dates on rocks and fossils
Questions for discussion
The age of fossils intrigues almost everyone. Students not only want to know how old a fossil is, but they want to know how that age was determined. Some very straightforward principles are used to determine the age of fossils. Students should be able to understand the principles and have that as a background so that age determinations by paleontologists and geologists don't seem like black magic.
There are two types of age determinations. Geologists in the late 18th and early 19th century studied rock layers and the fossils in them to determine relative age. William Smith was one of the most important scientists from this time who helped to develop knowledge of the succession of different fossils by studying their distribution through the sequence of sedimentary rocks in southern England. It wasn't until well into the 20th century that enough information had accumulated about the rate of radioactive decay that the age of rocks and fossils in number of years could be determined through radiometric age dating.
This activity on determining age of rocks and fossils is intended for 8th or 9th grade students. It is estimated to require four hours of class time, including approximately one hour total of occasional instruction and explanation from the teacher and two hours of group (team) and individual activities by the students, plus one hour of discussion among students within the working groups.
Fig#1
Purpose and objectives
This activity will help students to have a better understanding of the basic principles used to determine the age of rocks and fossils. This activity consists of several parts. Objectives of this activity are:
1) To have students determine relative age of a geologically complex area.
2) To familiarise students with the concept of half-life in radioactive decay.
3) To have students see that individual runs of statistical processes are less predictable than the average of many runs (or that runs with relatively small numbers involved are less dependable than runs with many numbers).
4) To demonstrate how the rate of radioactive decay and the buildup of the resulting decay product is used in radiometric dating of rocks.
5) To use radiometric dating and the principles of determining relative age to show how ages of rocks and fossils can be narrowed even if they cannot be dated radiometrically.
Materials required for each group
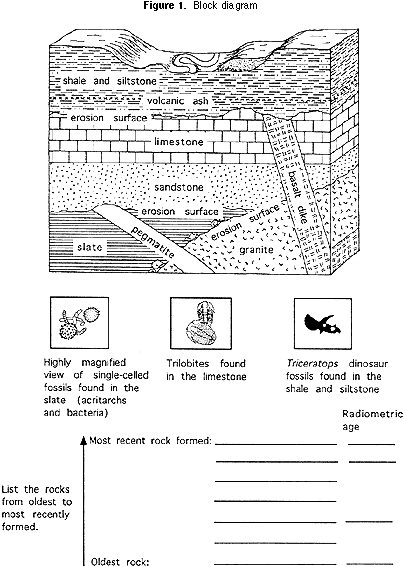
1) Block diagram (Figure 1).
2) Large cup or other container in which M & M's can be shaken.
3) 100 M & M's
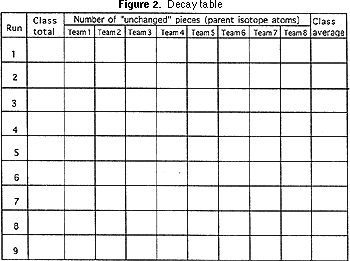
4) Graph paper (Figure 2).
5) Watch or clock that keeps time to seconds. (A single watch or clock for the entire class will do.)
6) Piece of paper marked TIME and indicating either 2, 4, 6, 8, or 10 minutes.
7) 128 small cards or buttons that may be cut from cardboard or construction paper, preferably with a different color on opposite sides, each marked with "U-235" all on one colored side and "Pb-207" on the opposite side that has some contrasting color.

Part 1: Determining relative age of the rocks
Each team of 3 to 5 students should discuss together how to determine the relative age of each of the rock units in the block diagram (Figure 1). After students have decided how to establish the relative age of each rock unit, they should list them under the block, from most recent at the top of the list to oldest at the bottom. The teacher should tell the students that there are two basic principles used by geologists to determine the sequence of ages of rocks.
They are:
Principle of superposition: Younger sedimentary rocks are deposited on top of older sedimentary rocks.
Principle of cross-cutting relations: Any geologic feature is younger than anything else that it cuts across.
Part 2: Radiometric age dating
Some elements have forms (called isotopes) with unstable atomic nuclei that have a tendency to change, or decay. For example, U-235 is an unstable isotope of uranium that has 92 protons and 153 neutrons in the nucl eus of each atom. Through a series of changes within the nucleus, it emits several particles, ending up with 82 protons and 125 neutrons. This is a stable condition, and there are no more changes in the atomic nucleus. A nucleus with that number of protons is called lead (chemical symbol Pb). The protons (82) and neutrons (125) total 207. This particular form (isotope) of lead is called Pb-207. U-235 is the parent isotope of Pb-207, which is the daughter isotope. Many rocks contain small amounts of unstable isotopes and the daughter isotopes into which they decay. Where the amounts of parent and daughter isotopes can be accurately measured, the ratio can be used to determine how old the rock is, as shown in the following activities.

Part 2a Activity — At any moment there is a small chance that each of the nuclei of U-235 will suddenly decay. That chance of decay is very small, but it is always present and it never changes. In other words, the nuclei do not "wear out" or get "tired". If the nucleus has not yet decayed, there is always that same, slight chance that it will change in the near future.
Atomic nuclei are held together by an attraction between the large nuclear particles (protons and neutrons) that is known as the "strong nuclear force", which must exceed the electrostatic repulsion between the protons within the nucleus. In general, with the exception of the single proton that constitutes the nucleus of the most abundant isotope of hydrogen, the number of neutrons must at least equal the number of protons in an atomic nucleus, because electrostatic repulsion prohibits denser packing of protons. But if there are too many neutrons, the nucleus is potentially unstable and decay may be triggered. This happens at any time when addition of the fleeting "weak nuclear force" to the ever-present electrostatic repulsion exceeds the binding energy required to hold the nucleus together.
Very careful measurements in laboratories, made on VERY LARGE numbers of U-235 atoms, have shown that each of the atoms has a 50:50 chance of decaying during about 704,000,000 years. In other words, during 704 million years, half the U-235 atoms that existed at the beginning of that time will decay to Pb-207. This is known as the half life of U- 235. Many elements have some isotopes that are unstable, essentially because they have too many neutrons to be balanced by the number of protons in the nucleus. Each of these unstable isotopes has its own characteristic half life. Some half lives are several billion years long, and others are as short as a ten-thousandth of a second.
A tasty way for students to understand about half life is to give each team 100 pieces of "regular" M & M candy. On a piece of notebook paper, each piece should be placed with the printed M facing down. This represents the parent isotope. The candy should be poured into a container large enough for them to bounce around freely, it should be shaken thoroughly, then poured back onto the paper so that it is spread out instead of making a pile. This first time of shaking represents one half life, and all those pieces of candy that have the printed M facing up represent a change to the daughter isotope. The team should pick up and set aside ONLY those pieces of candy that have the M facing up. Then, count the number of pieces of candy left with the M facing down. These are the parent isotope that did not change during the first half life.
The teacher should have each team report how many pieces of parent isotope remain, and the first row of the decay table (Figure 2) should be filled in and the average number calculated. The same procedure of shaking, counting the "survivors", and filling in the next row on the decay table should be done seven or eight more times. Each time represents a half life.
After the results of the final "half life" of the M& M are collected, the candies are no longer needed.
Each team should plot on a graph (Figure 3) the number of pieces of candy remaining after each of their "shakes" and connect each successive point on the graph with a light line. On the same graph each team should plot the AVERAGE VALUES for the class as a whole and connect that by a heavier line. AND, on the same graph, each group should plot points where, after each "shake" the starting number is divided by exactly two and connect these points by a differently colored line. (This line begins at 100; the next point is 100/ 2, or 50; the next point is 50/2, or 25; and so on.)

After the graphs are plotted, the teacher should guide the class into thinking about:
1) Why didn't each group get the same results?
2) Which follows the mathematically calculated line better? Is it the single group's results, or is it the line based on the class average? Why?
3) Did students have an easier time guessing (predicting) the results when there were a lot of pieces of candy in the cup, or when there were very few? Why?
U-235 is found in most igneous rocks. Unless the rock is heated to a very high temperature, both the U-235 and its daughter Pb-207 remain in the rock. A geologist can compare the proportion of U-235 atoms to Pb-207 produced from it and determine the age of the rock. The next part of this exercise shows how this is done.
Part 2b Activity — Each team receives 128 flat pieces, with U-235 written on one side and Pb-207 written on the other side. Each team is given a piece of paper marked TIME, on which is written either 2, 4, 6, 8, or 10 minutes.
The team should place each marked piece so that "U-235" is showing. This represents Uranium-235, which emits a series of particles from the nucleus as it decays to Lead-207 (Pb- 207). When each team is ready with the 128 pieces all showing "U-235", a timed two-minute interval should start. During that time each team turns over half of the U-235 pieces so that they now show Pb-207. This represents one "half-life" of U-235, which is the time for half the nuclei to change from the parent U-235 to the daughter Pb-207.
A new two-minute interval begins. During this time the team should turn over HALF OF THE U-235 THAT WAS LEFT AFTER THE FIRST INTERVAL OF TIME. Continue through a total of 4 to 5 timed intervals.
However, each team should STOP turning over pieces at the time marked on their TIME papers. That is, each team should stop according to their TIME paper at the end of the first timed interval (2 minutes), or at the end of the second timed interval (4 minutes), and so on. After all the timed intervals have occurred, teams should exchange places with one another as instructed by the teacher. The task now for each team is to determine how many timed intervals (that is, how many half-lives) the set of pieces they are looking at has experienced.
The half life of U-235 is 704 million years. Both the team that turned over a set of pieces and the second team that examined the set should determine how many million years are represented by the proportion of U-235 and Pb-207 present, compare notes, and haggle about any differences that they got. (Right, each team must determine the number of millions of years represented by the set that they themselves turned over, PLUS the number of millions of years represented by the set that another team turned over.)
Part 3: Putting dates on rocks and fossils
For the block diagram (Figure 1) at the beginning of this exercise, the ratio of U-235:Pb-207 atoms in the pegmatite is 1:1, and their ratio in the granite is 3:1.
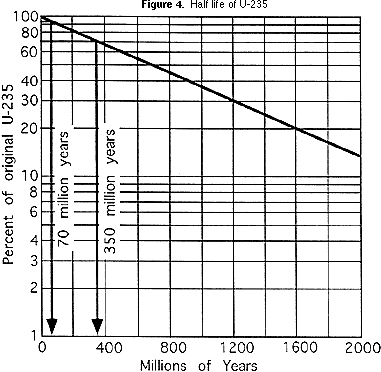
Using the same reasoning about proportions as in Part 2b above, students can determine how old the pegmatite and the granite are. They should write the ages of the pegmatite and granite beside the names of the rocks in the list below the block diagram (Figure 1). By plotting the half life on a type of scale known as a logarithmic scale, the curved line like that for the M & MTM activity can be straightened out, as you can see in the graph in Figure 4.
This makes the curve more useful, because it is easier to plot it more accurately. That is especially helpful for ratios of parent isotope to daughter isotope that represent less than one half life. For the block diagram (Figure 1), if a geochemical laboratory determines that the volcanic ash that is in the siltstone has a ratio of U-235:Pb-207 of 47:3 (94% of the original U-235 remains), this means that the ash is 70 million years old (see Figure 4). If the ratio in the basalt is 7:3 (70% of the original U-235 remains), then the basalt is 350 million years old (again, see Figure 4). Students should write the age of the volcanic ash beside the shale, siltstone and basalt on the list below the block diagram.
Questions for discussion
1) Based on the available radiometric ages, can you determine the possible age of the rock unit that has acritarchs and bacteria? What is it? Why can't you say exactly what the age of the rock is?
2) Can you determine the possible age of the rock unit that has trilobites? What is it? Why can't you say exactly what the age of the rock is?
3) What is the age of the rock that contains the Triceratops fossils? Why can you be more precise about the age of this rock than you could about the ages of the rock that has the trilobites and the rock that contains acritarchs and bacteria? Note for teachers: Based on cross-cutting relationships, it was established that the pegmatite is younger than the slate and that the slate is younger than the granite. Therefore, the slate that contains the acritarch and bacteria is between 704 million years and 1408 million years old, because the pegmatite is 704 million years old and the granite is 1408 million years old. The slate itself cannot be radiometrically dated, so can only be bracketed between the ages of the granite and the pegmatite.
The trilobite-bearing limestone overlies the quartz sandstone, which cross-cuts the pegmatite, and the basalt cuts through the limestone. Therefore the trilobites and the rock that contains them must be younger than 704 million years (the age of the pegmatite) and older than 350 million years (the age of the basalt). The limestone itself cannot be radiometrically dated, so can only be bracketed between the ages of the granite and the pegmatite.
The Triceratops dinosaur fossils are approximately 70 million years old, because they are found in shale and siltstone that contain volcanic ash radiometrically dated at 70 million years. Any Triceratops found below the volcanic ash may be a little older than 70 million years, and any found above may be a little younger than 70 million years. The age of the Triceratops can be determined more closely than that of the acritarchs and bacteria and that of the trilobites because the rock unit that contains the Triceratops can itself be radiometrically dated, whereas that of the other fossils could not.

