Maps and Scales
Maps and Scales
1. Types of Map Scales
2. Converting Between Scale Types
- Verbal Scale to RF
- Verbal Scale to Graphic Scale
- RF to Graphic Scale
- RF to Verbal Scale
- Graphic Scale to RF
3. Determining Scale from a Map or Photo
4. Determining Distance and Area from Map &
Scale
A.Finding area measurement from map and scale
B. Measurement Scales
C. Accuracy, Precision, and Significant Digits
D. Classification, Simplification and
Symbolization of Data
Source:
Map scale is the relationship between a unit of length on a map and the corresponding length on the ground. We will use concepts of map scale throughout the course, so it will pay you to study this section carefully.
1. Types of Map Scales
We can relate map and ground with three different types of scale.
- Verbal scale expresses in words a relationship between a map
distance and a ground distance. Usually it is along the lines of:
One inch represents 16 miles. Here it is implied that the one inch is on the map, and that one inch represents 16 miles on the ground. Verbal scales are commonly found on popular atlases and maps. - The second type of scale is a graphic scale, or bar scale. This shows directly on the map the corresponding ground distance.
For example:
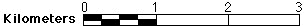
- The third type of scale is a representative fraction, or ratio scale. Compared to the first two, it is the most abstract, but also the most versatile. A representative fraction, or RF, shows the relationship between one of any unit on the map and one of the same unit on the ground. RFs may be shown as an actual fraction, for example 1/24,000, but are usually written with a colon, as in 1:24,000. In this example, one unit of any length (one mm, one cm, one inch, one foot, etc.) on the map represents 24,000 of those same units on the ground (24,000 mm, 24,000 cm, 24,000", 24,000', etc.). The RF is versatile because you are not tied to any specific units. You may work in any unit you choose, either metric, English, or other.
The RF is a called a fraction because it is just that--a fraction that shows how much the real world is reduced to fit on the map. A good comparison is often made with scale models of automobiles or aircraft. A 1/32-model of an auto is 1/32nd as large as the actual auto. In the same way, a 1:100,000-scale map is 1/100,000th as large as the ground area shown on the map.
A related idea is that of small scale versus large scale. Geographers use these terms differently than many people. A large scale map is where the RF is relatively large. A 1:1200 map is therefore larger scale than a 1:1,000,000 map. The 1:1,000,000 map would usually be called a small scale map. This is true even though the 1:1,000,000 map would show a much larger area than the 1:1200 map.
Here is a rule of thumb for size of scale by RF:
| Size of Scale | Representative Franction (RF) |
|---|---|
| Large Scale | 1:25,000 or larger |
| Medium Scale | 1:1,000,000 to 1:25,000 |
| Small Scale | 1:1,000,000 or smaller |
Of course, what is small or large scale is relative. I noticed a surveying text (Brinker & Wolf, 1984) that classed anything smaller than 1:12,000 as small scale -- surveyors rarely work with anything smaller than this.
The large/small scale terminology can become confusing when talking about large versus small areas. If you are talking about a phenomenon that occurs across a large region, it is tempting to say it's a large-scale phenomenon (e.g., "the forest blight is a large-scale disease"). But since the map that would show this would be small-scale, it is better to use a different term to avoid confusion. My favorite is "broad-scale."
Many maps include two or even all three types of scales. USGS topographic maps have both bar scales and RFs.
2. Converting Between Scale Types
If you are given one type of scale, you should be able to derive or construct any of the other two. This takes some practice, and some problems are included in your lab exercises. Some examples are given below.A vital step in doing any kind of conversion that involves differing units is to include the units in the problem itself. You can then cancel the units by multiplying or dividing. This way you avoid becoming confused about which conversion factors to use and how to use them.
Verbal Scale to RF
The key here is to write the verbal scale as a fraction, then convert so that both numerator and denominator have the same units, and the numerator has a 1.(a) Convert verbal scale of "1" to 18 miles" to RF
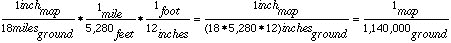
or 1:1,140,000.
Notice that the resulting fraction is rounded so that the RF does not imply more accuracy than the original precision warranted.
(b) Convert verbal scale of "15 cm to 1 km" to RF
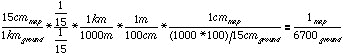
or 1:6700.
In many conversions you can save steps if you remember additional equivalencies.
For example, in (a) above, we could have used the fact that 1 mile = 63,360 inches to skip a step.
Verbal Scale to Graphic Scale
Usually this is a relatively easy task if the map gives us reasonable units in the verbal scale. We can use the verbal scale like a fraction to transform the ground distance to map distance.(c) Convert verbal scale of "1 cm to 14 km" to a graphic scale. One centimeter is a relatively small distance, so we probably don't want our bar scale to have major divisions much smaller than this. A centimeter represents 14 km, so a division of 10 km is probably fine. Therefore we want to find how many centimeters represent 10 km.
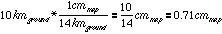
In other words, we can represent our 10 km increment on the bar scale by measuring off 0.71 cm on the map. We'd draw the first tick at 0.71 cm, the second at 1.42 cm, and so on:

RF to Graphic Scale
This adds an extra step to the example above. We can find the map-distance equivalent of a ground distance, but we also need to be careful about choosing which ground distance we want to portray on the map. Perhaps it's easiest to choose a smaller ground distance that you can then multiply to get a reasonable bar scale.(d) Convert an RF of 1:250,000 to a graphic scale If we aren't sure what increments a bar scale would have for this scale, we could start out, say, with finding the map equivalent of 1 mile:
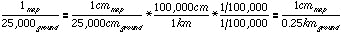
This might work fine, with one mile marked off on the map every 0.25 inch; or, we may want finer or broader increments, which we can find by dividing or multiplying the .25" as needed.
RF to Verbal Scale
Again we have to choose appropriate units to convert into. Most verbal scales are either "one inch represents ____ miles," or "one centimeter represents ___ kilometers." These are relatively easy to do, since it means only that we convert the denominator of our RF to the larger units.(e) Convert from RF of 1:25,000 to a verbal scale, in metric
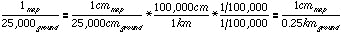
Therefore,
1 centimeter on this map represents 1/4 of a kilometer on the ground.
Graphic Scale to RF
Here we must take a measurement from the bar scale to determine the map distance that corresponds to a ground distance.(f) Find the RF scale for the following graphic scale

By measuring with a ruler, we find that 10 kilometers measures 2.4 cm. We can use this relationship to find the RF for the bar scale:
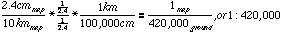
3. Determining Scale from a Map or Photo
Some maps may come with no scale at all. Aerial photographs almost never do (unless one was painted on the ground before the photo was taken!). How can you derive a scale for use with the map or photo?Actually the procedure is very similar to the last example above. But instead of measuring along a bar scale, you must measure the length of an object on the map or photo whose actual length you know. This might be a football field, a city block, or the Equator (if it's a world map). Often you can identify 1-mile-square sections in the US (see the account below, under Survey Systems). You may even need to go out to the location mapped or pictured and measure the distance between two identifiable objects.
Once you have the two distances, you can find the scale as above. For another example, suppose you have a map where the distance between two section-line roads is 3.5 inches on the map. We can usually assume this is one mile on the ground (there are exceptions). The RF scale is then:
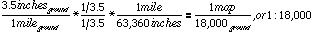
One caveat (exception) for air photos is that this method assumes the two locations are at the same elevation--or that the terrain is flat. If you are using air photos, the terrain may not be flat. If there are hills, even moderate ones, the calculations can be thrown off. Keep this in mind for later in the course.
Another way to calculate scale on an unknown map or photo is to compare it to a map with a known scale. For example, suppose you have an air photo where the distance between two hills is 7.2 centimeters.You have a map of the same area at 1:24,000, and on the map the distance between the hills is 2.4 centimeters.
The answer involves a little algebra. Since the ground distance is the same on both photo and map, we can create an expression for this ground distance for both, and then put them on either side of an equation. The ground distance can be found by multiplying the map/photo distance by the scale (in this case, by the inverse of the scale--notice how this makes the units cancel correctly). We need to find, for the photo, how many ground units are represented by one unit on the photo, so we use an x for this unknown quantity and solve for it:
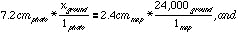
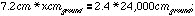
we can cancel the units on each side and divide by 7.2:
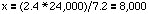 In other words, the RF scale for the
photo is 1:8,000.
In other words, the RF scale for the
photo is 1:8,000.4. Determining Distance and Area from Map & Scale
Map scale isn't much use in and of itself. We can use a map's scale to determine distances and areas on the map. Compared to converting between scale types, calculating distance is simple. Area calculations are trickier, since we have to square the numbers.Finding distance from map and scale
As an example, suppose we have a map with a scale of 1:50,000. We measure the distance along a property boundary as 1.7 cm. What is the length in the real world?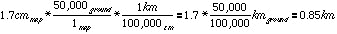
To find ground distance, we must use the map scale to convert map distance to ground distance. Notice that again we inverted the RF scale, so the units will cancel properly. Once we multiply by the scale, we need to convert the ground distance to units suitable for ground measurement--in this case, from centimeters to kilometers.
We can also calculate distance from verbal and graphic scales. With verbal scales, we use the same procedure as above with the RF. The only difference is that we have to use the units given in the verbal scale (e.g., 1 inch to 17 miles). We'd probably want to measure our map distance in the same units (in this case, inches) to make our conversion easy.
Graphic scales are probably the scales most frequently used by laypersons. You can mark off a distance on the map and compare it directly to the bar scale. You need not know how many inches or centimeters the map distance is. The main drawback of bar scales is that they are usually short compared to the map itself, and hence measuring longer distances is difficult.
A. Finding area measurement from map and scale
Area must be expressed in areal units, which are usually distance units squared -- cm2 , mi2, and so on. We must therefore used squared conversion factors when finding area from map measurements.
For example, suppose we measure a rectangular piece of property that is 3 cm by 4 cm on a map. The map is at a scale of 1:24,000. What is the area of the parcel?
The area of the parcel on the map is

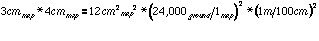
on the ground.
Since this is a large number, we might want to translate to other units. There are 10,000 square meters per hectare, so the area is 69 hectares (ha) (a hectare is about 2.5 acres). Or, there are (1,000)2 = 1,000,000 square meters per square kilometer, so the area is also 0.69 km2.
Notice that by writing the units as part of the problem, and squaring them along with the numbers, our units cancel properly and we end up with a sensible answer.
There is another way to tackle area problems if you have distance dimensions like 3 x 4 cm to start out the problem. You can convert the distance dimensions to real-world distances first, and then multiply them to find the area. This makes the problem longer but perhaps simpler.
B. Measurement Scales
1. Definition
Any type of information on a map (or in a table, a list, a survey, etc.) can be described in terms of how pieces of the information can be related to each other. Examples of mapped information include land-use classes, road classes, city populations, and county areas.We can think of these types of information as either categorical (or qualitative) or numerical (or quantitative). Categorical information can only be described qualitatively, whereas items of numerical information can be compared quantitatively. That is, numerical information is on a real scale, such as distance (e.g., kilometers), area (e.g., hectares), or temperature (e.g., Celsius).
- Example of categorical information:
- Land-Use categories of :
- 1= forest, 2 = grassland, 3 = urban;
- We cannot say that based on the classes, 1 + 2 = 3 !
- We can only use the numbering to describe the items qualitatively.
- Example of Numerical information, city populations:
- Springfield = 100, Harmony = 200, Centerville = 300;
- We can say that Centerville has as many people as Springfield and Harmony.
2. Four Measurement Levels
The categorical and numerical types have traditionally been further broken down, each into two levels of measurement:Categorical information can either be nominal level or ordinal level . At the nominal level, categories simply describe different types of things, and cannot be compared to each other. Ordinal-level categories can, on the other hand, be ranked against each other.
An example of ordinal level would be road classes of interstate, primary, secondary, and primitive; although two primary roads don't make an interstate, you could say in a sense that interstates are at a higher level than the others, at least in terms of expense to build!
The land-use classes would be an example of nominal-level measurement. You probably wouldn't rank the classes against each other (unless you prefer one over the other, in which case they could be ordinal!).
Numerical information can either be interval level or ratio level . This distinction is subtle, and borders on artificial. The only difference is that ratio-level information is on a scale that includes a true zero, that is, a zero that truly represents a lack of whatever it is you're measuring.
One of the few common examples of an interval scale is temperature. You can compare two temperature readings quantitatively. For example, 20 C is 15 degrees warmer than 5 C. But the Celsius scale has an arbitrary zero point (the freezing temperature of water, or 32 F). 0 C doesn't mean a lack of temperature. For this reason, 20 C is not four times as warm as 5 C! (One temperature scale, Kelvin, does feature a true zero -- 0 K is -273 C, the temperature at which all molecular motion ceases). Fortunately, there are few examples of this on maps. You might want to include an exception for elevation, which can be below sea level, or longitude, where the 0° line (Prime Meridian) is arbitrarily drawn on the globe.
Table 2: Measurement Levels
| Measurement Level |
Description |
Examples |
|
| Categorical |
Nominal |
Simple categories; cannot rank categories |
Colors; land use types; computer components |
| Categorical |
Ordinal |
Distinct categories; can rank categores in order |
Road classes; flavor preferences |
| Numerical |
Interval |
Continuous scale; measure with numbers; real zero |
Temperature; longitude, compass direction |
| Numerical |
Ratio |
Continuous scale; measure with numbers; real zero |
Distance; weight; bank balance |
3. So What?
We will use this terminology frequently to describe the kinds of information on maps and in other sources. You will also encounter it elsewhere, I guarantee it!Information often is translated from one level to another. The general rule is that it's easier to translate to a lower level (e.g., from ratio to ordinal) than to a higher level. In most cases, it's impossible to go legitimately to a higher level. Why bother using a lower-level scale? Often it saves space and energy to use a lower scale.
For example, if you have a table of city populations in Sonoma County (i.e., ratio level) and want to show population on a map, you could print a number next to each city name. This would preserve your ratio-level data on the map itself. A more common technique is to have a set of increasingly large symbols for the city location, each symbol indicating a range of population. These symbols would give ordinal-level information about population. This conveniently reduces the clutter on the map, but you cannot recover the original ratio-level numbers from the map.
C. Accuracy, Precision, and Significant Digits
1. Accuracy versus Precision
Some people make a distinction between accuracy and precision.
Accuracy would be how close a measured value is to the actual value.
Precision would be the number of digits reported with the value. For example, I added a thermometer to my car that shows the outside temperature to tenths of a degree (e.g., 65.2° F). The thermometer's precision is to tenths of a degree Fahrenheit. But it often seems to give readings that are too high, perhaps due to the engine's heat nearby. Its accuracy, then, might only be to within 5° F.
2. Significant Digits
Significant digits are the number of digits in a value that have real meaning and reflect the accuracy of the value or measurement. For example, a distance measurement of 45.8 km would have three significant digits. The value implies that the measurement was made to an accuracy of tenths of a kilometer. If the instrument, such as an odometer, is not accurate, the value should not include as many significant digits. Of course, if the instrument measures more accurately than this, the value should be reported with the appropriate precision.
The main point is to beware measurements with highly precise values when the accuracy could be called into question. This is especially true when converting values from one kind of scale to another. For example, if I measure a map distance as 11 inches with an ordinary ruler, then want to convert to centimeters, I find on my calculator:
(11 in.) * (2.54 cm/in.) = 27.94 cm But 27.94 cm implies high accuracy, which I didn't have with the original measurement. The solution here is to round the answer to about the same number of significant digits as the original measurement. In this case, I should probably say the distance is 28 cm.
More example of significant digits:
- Two significant digits: 3700, 37, 3.7, 0.37, 0.0037
- Four significant digits: 19120, 19.12, 0.001912, 19.00, 0.1900
Another solution is to use scientific notation.
For example, 3700 with the zeroes actually being significant can be written as 3.700 x 103. This breaks the number down into the mantissa (the significant digits, here 3.700) and the exponent on the ten (here 3). In scientific notation, only one digit is placed before the decimal point in the mantissa. The exponent on the 10 indicates how many places the decimal point should be moved to restore the number to ordinary notation (in this case, three places to the right; this is equivalent to multiplying the mantissa by 1000). Negative exponents mean smaller numbers, and we shift the decimal point to the left. For example, 3.700 x 10-4 is the same as 0.0003700. Scientific notation is handy with very large or small numbers. Numbers in scientific notation can be used just like other numbers, as long as you follow the rules of exponents -- for multiplying, dividing, etc.
D. Classification, Simplification and Symbolization of Data
This is not a course in cartography, so we will not deal in detail with how data is classified and simplified for mapping, and how symbols are created to suit those data. But you should be aware that any map, including topographic maps, is the result of a lot of processing of the data behind the map. Here is a brief discussion of some elements that go into data processing for maps.1. Classification
Maps must take the relevant data and assign it to a given number of classes, each with its own number of members. Examples are maps of land uses and of temperature. For categorical data like land uses, it is easy to overload the map reader with too many classes. Cartographers recommend a maximum of five or six different classes (for land use, these might be forest, rangeland, cropland, water, and urban). Numerical data shown on isarithmic maps (which show zones of equal values) can be somewhat more complex. For example, temperature zones can trend from 80's F to -20's F. But the data should be shown with logical symbolization (see below).Data can be broken down into categories in three ways:
(a) Each category can have an equal number of members. For example, in a map of US population by state, we could have five categories of population, each with ten states.
(b) Each category could span an equal interval of values. In the population map, we would take the range of populations (highest state minus lowest state), and divide the range by five. Each category would be one-fifth of the overall range. In this map, categories may have different numbers of states. The highest category may only have a few states (e.g., California, New York and Texas), and other categories may have a large number of states.
(c) Finally, we could subjectively assign states to classes, perhaps by looking for "natural breaks" in population rankings. Often map-makers start out with one of the first two methods, then refine it by looking at the results and changing classes slightly. All of this should reflect the purposes of the map. Different methods can produce radically different-looking maps (see any cartography text for examples).
2. Simplification
A second major task in map-making is simplifying the information behind the map. Classification is one way of simplifying the data we use going into the map. Often this involves lowering the measurement level of the data (such as transforming ratio-level data to ordinal-level data, as in our example of city populations indicated by various circle sizes).Another simplification task relates to the spatial aspects of the data. For example, mountainous roads may take many twists and turns. A map that shows all these curves would be cluttered and messy. We may want to generalize the road spatially to clarify things. Beware, of course, those map users who curse you for those curves they didn't expect! The cartographer's job is to simplify without distorting and misleading the map user.
Sometimes the task may necessitate eliminating features altogether. For example, a small-scale US map can show only selected cities; how do you choose which cities to include without offending too many people? I saw a US map recently that included moderate-sized cities but omitted my hometown, San Diego (now the 6th largest city in the US).
3. Symbolization
Symbolization of information is another crucial part of communicating through maps. What symbols are chosen will influence whether will people will understand, or even use, a map. Symbols should be chosen so that the intended audience will understand them. Different symbols should be used for general-purpose maps than those intended for specialists in a field.Symbols can be placed on a continuum between intuitive and abstract. Intuitive symbols suggest to the reader what they represent. Pictographs are recognizable representations of the actual objects. For example, marshes are often shown with swampy grass symbols, or airports as planes. On the other extreme are abstract symbols with no obvious connection to what they represent. Examples are circles as cities, or streams as dotted lines. Some abstract symbols have been used so widely to represent a particular feature that, although abstract, they do connect with the object in most people's minds. A star within a circle, for instance, usually means a capital city.
Symbols can also be classed according to their dimension: point (0-dimension), line (1-dimension) or area (2-dimension) symbols. Like the other two, point symbols can convey categorical or numerical information. Examples of categorical point symbols are airports, campgrounds, springs, and quarries. Variable-sized circles for city population would be examples of numerical point symbols.
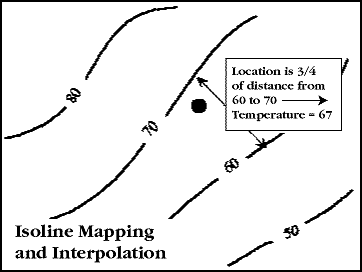
Line symbols can convey information about linear features, such as roads, railroads, and streams. Another important use of lines on maps are isolines. Isolines (also called isarithms) connect points of equal value. You'll often see these on a map of temperatures on the weather page of the newspaper. Every place along an isoline on this map has the same temperature, at least theoretically. This implies also that places between two isolines have values somewhere between the values of the surrounding lines. Without additional information, we cannot say with confidence much more about intervening values. We can estimate, or interpolate, the intervening values, for example by measuring the distance of a point from each line. There is no guarantee, of course, that our estimate is really correct, so beware such estimates from isoline maps.
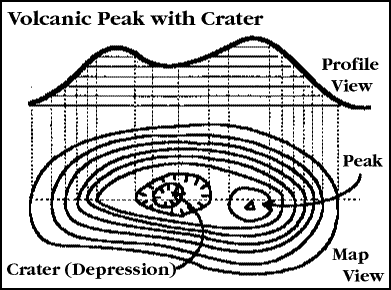
An important type of isoline for this course is the elevation contour . These isolines show equal elevations, and are included on all USGS topographic maps. The contour interval is the height difference between each contour. Contour intervals on USGS maps vary depending upon the terrain. Common intervals on 1:24,000-scale maps are 20, 40 and 80 feet. A 20-foot interval would show, for example, contours at 0 (sea level), 20, 40, 60, 80, and so on.
It takes some practice to feel comfortable working with elevation contours and other isoline maps. We will have lab exercises to give you some practice with them, including visualizing terrain and constructing profiles, or two-dimensional views of how elevation changes on a line across the topographic map.
The zones between isolines are often shaded or colored to portray the information more effectively. Temperature maps in most newspapers are now in color, with warmer zones getting "warmer" colors, colder areas "cooler" colors. These shaded-isoline zones are a blend of line and area symbols.
Speaking of color and shading, let us cover one final point about map symbolization. The rules about using color and shading are different for nominal versus higher-level data (ordinal, interval, and ratio). If you are mapping nominal-level data, the categories have no particular order, and you probably want to maximize the contrast between categories. Land uses, for example, should be portrayed so that you can separate urban, suburban, forest, and pasture, or whatever categories you include on the map.
Ordinal, interval or ratio data should be mapped differently. Here there is a definite ordering of categories. To use the temperature map again, we have a trend from warm to cold in the zones we portray. We want the map reader to immediately appreciate this gradual trend in the data. Therefore we select an ordering of colors or symbols that conveys this continuous trend in the data, for example: red-orange-yellow-green-blue-violet.
Many people make the mistake of thinking they should select colors that maximize contrast between categories, even with ordinal or higher-level data. Beware this mistake! You may be able to pick out categories easily with this approach, but you destroy the impression of a trend in the data.

